题目内容
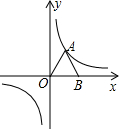 如图,等边△OAB的边长为2,点B在x轴上,反比例函数图象经过A点,将△OAB绕点O顺时针旋转a度(0<a<360),使点A落在双曲线上,则a=
如图,等边△OAB的边长为2,点B在x轴上,反比例函数图象经过A点,将△OAB绕点O顺时针旋转a度(0<a<360),使点A落在双曲线上,则a=考点:反比例函数图象上点的坐标特征,坐标与图形变化-旋转
专题:
分析:根据双曲线的轴对称性和中心对称性即可求解.
解答:解:根据反比例函数的轴对称性,A点关于直线y=x对称,
∵△OAB是等边三角形,
∴∠AOB=60°,
∴AO与直线y=x的夹角是15°,
∴a=2×15°=30°时点A落在双曲线上,
根据反比例函数的中心对称性,
∴点A旋转到直线OA上时,点A落在双曲线上,
∴此时a=180°,
根据反比例函数的轴对称性,继续旋转30°时,点A落在双曲线上,
∴此时a=210°;
故答案为30°或180°或210°.
∵△OAB是等边三角形,
∴∠AOB=60°,
∴AO与直线y=x的夹角是15°,
∴a=2×15°=30°时点A落在双曲线上,
根据反比例函数的中心对称性,
∴点A旋转到直线OA上时,点A落在双曲线上,
∴此时a=180°,
根据反比例函数的轴对称性,继续旋转30°时,点A落在双曲线上,
∴此时a=210°;
故答案为30°或180°或210°.
点评:本题考查了反比例函数的综合运用,旋转的性质.关键是通过旋转及双曲线的对称性得出结论.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下面四个方程中,与方程x-1=2的解相同的是( )
| A、2x=-6 |
| B、x+2=-1 |
| C、2x+1=3 |
| D、-3x=-9 |
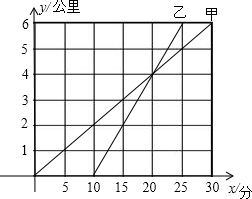 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,如图是行驶过程中路程y与时间x的关系的图象.根据图象,回答下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,如图是行驶过程中路程y与时间x的关系的图象.根据图象,回答下列问题: 如图,已知△ABC的面积为4cm2,它的三条中位线组成△DEF,△DEF的三条中位线组成△MNP,则△MNP的面积等于多少?
如图,已知△ABC的面积为4cm2,它的三条中位线组成△DEF,△DEF的三条中位线组成△MNP,则△MNP的面积等于多少? 如图,已知AB∥DC,AD∥BC,求证:AB=CD.
如图,已知AB∥DC,AD∥BC,求证:AB=CD.