题目内容
14.正方形ABCD中,直线l经过点A,过点B、D分别作直线l的垂线,垂足分别为E、F,若BE=7,DF=4,则DE的长度为$\sqrt{137}$或5.分析 分l经过正方形外部和内部两种情况,可证得△ABE≌△DAF,则可求得AE和AF的长,则可求得EF的长,连接DE,在Rt△DEF中,利用勾股定理可求得答案.
解答 解:
当直线l在正方形外部时,如图1,连接DE,
∵BE⊥EF,DF⊥EF,
∴∠BEA=∠AFD=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠ABE=∠BAE+∠DAF=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中
$\left\{\begin{array}{l}{∠BEA=∠AFD}\\{∠ABE=∠DAF}\\{AB=AD}\end{array}\right.$
∴△ABE≌△DAF(AAS),
∴AE=DF=4,AF=BE=7,
∴EF=AE+AF=11,
在Rt△DEF中,由勾股定理可得DE=$\sqrt{D{F}^{2}+E{F}^{2}}$=$\sqrt{{4}^{2}+1{1}^{2}}$=$\sqrt{137}$,
当直线l经过正方形内部时,如图2,连接DE,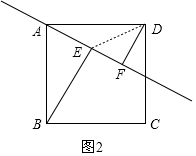
同理可证得△ABE≌△DAF,
∴AE=4,AF=7,
∴EF=AF-AE=3,
在Rt△DEF中,由勾股定理可得DE=5,
故答案为:$\sqrt{137}$或5.
点评 本题主要考查正方形的性质及全等三角形的判定和性质,利用条件证得全等三角形,求得AE和AF的长是解题的关键,注意分情况讨论.

练习册系列答案
相关题目
 如图,在长方体ABCD-EFGH中,与面ADHE平行的面是面BCGF.
如图,在长方体ABCD-EFGH中,与面ADHE平行的面是面BCGF.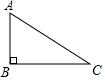 如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )
如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( ) 如图,E、F在双曲线y=$\frac{k}{x}$上,EF交y轴于点A,AE=EF,FM⊥x轴于点M,若S△AME=3,则k=-12.
如图,E、F在双曲线y=$\frac{k}{x}$上,EF交y轴于点A,AE=EF,FM⊥x轴于点M,若S△AME=3,则k=-12. 在一次爱心捐款中国,某班40,名学生捐款情况如扇形统计图所示,则这个班级的学生共捐款640元.
在一次爱心捐款中国,某班40,名学生捐款情况如扇形统计图所示,则这个班级的学生共捐款640元.