题目内容
15.为推广使用某种新型电子节能产品,国家对经营该产品的企业及个人给予资金补贴,某经销商在享受此优惠政策后,决定将销售价为每个30元的这种产品实行降价促销,在促销中发现,当每个产品的销售价降低x元时,日销售量y(个)与x(元)之间满足关系式y=10x+100,已知购进这种产品所需成本为每个10元.(1)用含x的代数式表示:降价后,每个产品的实际销售价为30-x元,每个产品的利润为20-x元;
(2)设降价后该产品每日的销售利润为W元,求W与x之间的函数关系式;
(3)若规定每个产品的降价不得超过10元,试问:当产品的日销售量最大时,每日的销售利润能否也最大?为什么?
分析 (1)根据题意容易得出每个产品的实际销售价和每个产品的利润;
(2)根据题意得出W=(20-x)(10x+100),即可得出结果;
(3)由一次函数的性质得出y随x的增大而增大,当产品的日销售量最大时,x=10,y=200,求出利润W;再把W与x的函数关系式化成顶点式,得出最值,即可得出结论.
解答 解:(1)根据题意得:降价后,每个产品的实际销售价为(30-x)元,
每个产品的利润为:30-x-10=20-x(元);
故答案为:30-x,20-x;
(2)根据题意得:W=(20-x)(10x+100)=-10x2+100x+2000,
即W与x之间的函数关系式为:y=-10x2+100x+2000;
(3)当产品的日销售量最大时,每日的销售利润不能最大;理由如下:
∵y=10x+100,y随x的增大而增大,若规定每个产品的降价不得超过10元,
当产品的日销售量最大时,x=10,y=100+100=200,
此时W=(20-10)×200=2000(元);
∵W=-10x2+100x+2000=-10(x-5)2+2250,
即当x=5时,W最大=2250>2000,此时y=150;
∴当产品的日销售量最大时,每日的销售利润不能最大.
点评 本题考查了二次函数的运用以及最值问题;根据题意得出二次函数的解析式是解决问题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
5.在下列各数0.51515354…、0、0.80108、$\sqrt{4}$、0.2、3π、$\frac{22}{7}$、6.1010010001…、$\frac{131}{11}$、$\sqrt{7}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.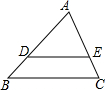 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
20. 如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
 如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )| A. | AD=CD | B. | AD=BC | C. | DC=2AB | D. | AB:BD=2:3 |
15.函数y=3x-6和y=-x+4的图象交于一点,这一点的坐标是( )
| A. | (-$\frac{5}{2}$,-$\frac{3}{2}$) | B. | ($\frac{5}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,$\frac{5}{2}$) | D. | (-2,3) |