题目内容
7. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )| A. | 4π-4 | B. | 2π-4 | C. | 4π | D. | 2π |
分析 首先证明S△AOE=S△OEB,可得S阴=S扇形OBC,由此即可解决问题.
解答 解:∵CD是直径,CD⊥AB,∠AOB=90°
∴AE=EB,∠AOE=∠BOC=45°,
∴S△AOE=S△OEB,
∴S阴=S扇形OBC=$\frac{45•π•{4}^{2}}{360}$=2π,
故选D.
点评 本题考查扇形的面积等计算、垂径定理等知识,解题的关键是灵活运用所学知识解决问题,学会把不规则图形转化为规则图形,属于中考常考题型.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.内角和与外角和相等的多边形是( )
| A. |  | B. |  | C. |  | D. |  |
2.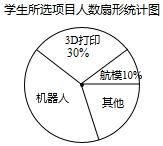 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
根据以上信息解决下列问题:
(1)m=8,n=3;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为144°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
 初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.男、女生所选项目人数统计表
| 项目 | 男生(人数) | 女生(人数) |
| 机器人 | 7 | 9 |
| 3D打印 | m | 4 |
| 航模 | 2 | 2 |
| 其他 | 5 | n |
(1)m=8,n=3;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为144°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
19.下列命题是假命题的是( )
| A. | 不在同一直线上的三点确定一个圆 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 正六边形的内角和是720° | |
| D. | 角的边越大,角就越大 |
17.下列所述图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五边形 | D. | 圆 |
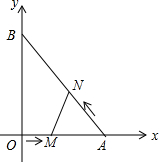 如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒$\frac{5}{3}$个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒$\frac{5}{3}$个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0). 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段BE=EA.
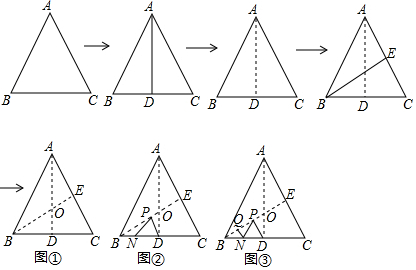
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段BE=EA. 我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈$\frac{L}{d}$=$\frac{6r}{2r}$=3,那么当n=12时,π≈$\frac{L}{d}$=3.11.(结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈$\frac{L}{d}$=$\frac{6r}{2r}$=3,那么当n=12时,π≈$\frac{L}{d}$=3.11.(结果精确到0.01,参考数据:sin15°=cos75°≈0.259)