题目内容
2.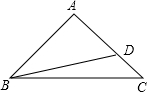 如图,在△ABC中,AB=AC=a,BC=b,∠A=100°,点D在AC边上,∠ABD=30°,则AD的长为$\frac{{a}^{2}}{b}$.
如图,在△ABC中,AB=AC=a,BC=b,∠A=100°,点D在AC边上,∠ABD=30°,则AD的长为$\frac{{a}^{2}}{b}$.
分析 以BC为边在△ABC的下面作等边三角形BCE,连接AE,由等腰三角形和等边三角形的性质得出AE⊥BC,CE=BC=b,∠BCE=60°,由等腰三角形的性质和三角形内角和定理得出∠ACB=∠ABC=50°,∠CAE=$\frac{1}{2}$∠BAC=50°,求出∠ADB=∠CAE,∠ACE=∠ACB+∠BCE=∠BAC,证出△ABD∽△CAE,得出对应边成比例,即可得出答案.
解答  解:以BC为边在△ABC的下面作等边三角形BCE,连接AE,如图所示:
解:以BC为边在△ABC的下面作等边三角形BCE,连接AE,如图所示:
则AE⊥BC,CE=BC=b,∠BCE=60°,
∵AB=AC,∠BAC=100°,
∴∠ACB=∠ABC=(180°-1100°)÷2=50°,∠CAE=$\frac{1}{2}$∠BAC=50°,
∵∠ABD=30°,
∴∠ADB=180°-∠BAC-∠ABD=50°,
∴∠ADB=∠CAE,∠ACE=∠ACB+∠BCE=100°=∠BAC,
∴△ABD∽△CAE,
∴$\frac{AD}{AB}=\frac{AC}{CE}$,即$\frac{AD}{a}=\frac{a}{b}$,
解得:AD=$\frac{{a}^{2}}{b}$;
故答案为:$\frac{{a}^{2}}{b}$.
点评 本题考查了等腰三角形的性质、等边三角形的性质、相似三角形的判定与性质、三角形内角和定理等知识;熟练掌握等腰三角形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
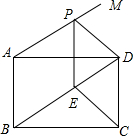 如图,矩形ABCD中,AB=6,BD=10,射线AM∥BD,点P是AM上一个动点,过点P作AB的平行线,交BD于点E.
如图,矩形ABCD中,AB=6,BD=10,射线AM∥BD,点P是AM上一个动点,过点P作AB的平行线,交BD于点E. 如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有①③④.
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有①③④.
 如图,从A地到B地共有五条路,你应选择第③条路(填标出的数字),因为两点之间线段最短.
如图,从A地到B地共有五条路,你应选择第③条路(填标出的数字),因为两点之间线段最短.