题目内容
 一个标有高度的圆柱形容器,加入一些水后观察水面高度
一个标有高度的圆柱形容器,加入一些水后观察水面高度如图(1)所示,这时将一个直径为2cm的圆柱玻璃棒竖直插至容器底部,水面高度如图(2)所示,求容器的内口直径(圆柱的容积=底面圆面积×高)
考点:算术平方根
专题:
分析:根据圆柱玻璃棒的直径求出圆柱形玻璃棒的底面半径,再根据圆柱形容器中水面上升部分的容积等于玻璃棒浸没在水中部分的体积,求出圆柱形容器的底面半径,从而得出容器的内口直径.
解答:解:∵圆柱玻璃棒的直径为2cm,
∴圆柱形玻璃棒的底面半径2÷2=1(cm),
∵圆柱形容器中水面上升部分的容积等于玻璃棒浸没在水中部分的体积,
设圆柱形容器的底面半径为r厘米,则有
πr2×(8-7)=π•12×8,
∴r2=8,
∴r=2
,
∴圆柱形容器的直径是:2×2
=4
(厘米).
∴圆柱形玻璃棒的底面半径2÷2=1(cm),
∵圆柱形容器中水面上升部分的容积等于玻璃棒浸没在水中部分的体积,
设圆柱形容器的底面半径为r厘米,则有
πr2×(8-7)=π•12×8,
∴r2=8,
∴r=2
| 2 |
∴圆柱形容器的直径是:2×2
| 2 |
| 2 |
点评:此题考查了算术平方根,熟练掌握算术平方根的意义和求出r的值是本题的关键.

练习册系列答案
相关题目
若1<x<2,则
+
的值等于( )
| ||
| x-2 |
| |x-1| |
| x-1 |
| A、2 | B、-2 | C、0 | D、±2 |
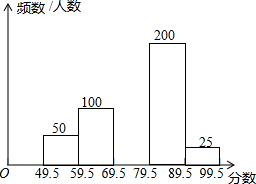 某市为了解参加历史科结业的2万名学生的考试成绩情况,现从中随机抽取部分学生的成绩作为一个样本,整理后分成5组,绘制了频数分布直方图,其中,第二组的频率为0.2.
某市为了解参加历史科结业的2万名学生的考试成绩情况,现从中随机抽取部分学生的成绩作为一个样本,整理后分成5组,绘制了频数分布直方图,其中,第二组的频率为0.2.