题目内容
11.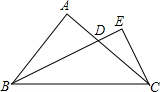 已知Rt△ABC,∠BAC=90°,AB=AC,过点B的直线BE交直线AC于D,CE⊥BE于E,当BE平分∠ABC,求证:①BD=2CE;②AB+AD=BC.
已知Rt△ABC,∠BAC=90°,AB=AC,过点B的直线BE交直线AC于D,CE⊥BE于E,当BE平分∠ABC,求证:①BD=2CE;②AB+AD=BC.
分析 (1)如图1,延长CE,BA交于F,根据已知条件得到∠BEF=∠BEC=90°,∠CBE=∠FBE,推出△CBE≌△FBE,由全等三角形的性质得到CE=EF,证得CF=2CE,通过△ABD≌△ACF,得到BD=CF,等量代换得到结论;
(2)如图2,过D作DH⊥BC于H,根据等腰直角三角形的性质得到∠ACB=45°,求得∠HDC=45°=∠ACB,根据等腰三角形的性质得到DH=CH,根据角平分线的性质得到AD=DH,证得Rt△ABD≌Rt△BDH,于是得到AB=BH,即可得到结论.
解答  证明:(1)如图1,延长CE,BA交于F,
证明:(1)如图1,延长CE,BA交于F,
∵CE⊥BE于E,当BE平分∠ABC,
∴∠BEF=∠BEC=90°,∠CBE=∠FBE,
在△CBE与△FBE中,
$\left\{\begin{array}{l}{∠FBE=∠CBE}\\{BE=BE}\\{∠BEF=∠BEC}\end{array}\right.$,
∴△CBE≌△FBE,
∴CE=EF,
∴CF=2CE,
∵∠BAC=90°,∠ADB=∠CDE,
∴∠ABD=∠ACE,
在△ABD与△ACF中,
$\left\{\begin{array}{l}{∠BAC=∠CAF}\\{AB=AC}\\{∠ABD=∠ACF}\end{array}\right.$,
∴△ABD≌△ACF,
∴BD=CF,
∴BD=2CE;
(2)如图2, 过D作DH⊥BC于H,
过D作DH⊥BC于H,
∵∠BAC=90°,AB=AC,
∴∠ACB=45°,
∴∠HDC=45°=∠ACB,
∴DH=CH,
∵BE平分∠ABC,
∴AD=DH,
∴AD=CH,
在Rt△ABD与Rt△BDH中,
$\left\{\begin{array}{l}{AD=DH}\\{BD=BD}\end{array}\right.$,
∴Rt△ABD≌Rt△BDH,
∴AB=BH,
∴BC=BH+CH=AB+AD.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,角平分线的性质,正确的作出辅助线是解题的关键.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 赚160元 | B. | 赔80元 | C. | 赔240元 | D. | 赚400元 |
| A. |  | B. |  | C. |  | D. |  |
 如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.
如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.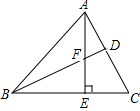 如图,AE是△ABC的高,D为AC上一点,AE交BD于点F,且FE=CE,BF=AC.求证:BD⊥AC.
如图,AE是△ABC的高,D为AC上一点,AE交BD于点F,且FE=CE,BF=AC.求证:BD⊥AC.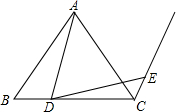 如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,
如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,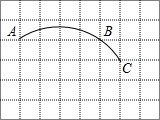 如图,边长为1的正方形网格中,一段圆弧经过网格的交点A,B,C.
如图,边长为1的正方形网格中,一段圆弧经过网格的交点A,B,C.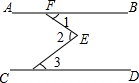 如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.
如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.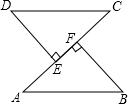 已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.