题目内容
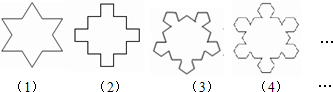
如图，第（1）个多边形由正三角形“扩展”而来，边数记为a3=12．第（2）个多边形由正方形“扩展”而来，边数记为a4=20，…，依此类推，由正n边形“扩展”而来的多边形的边数记为an（n≥3），则a5=______；求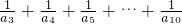
的结果是______．
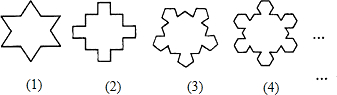
解：∵a3=12=3×4，a4=20=4×5，
∴a5=5×6=30．
∴=
-
+-
+…+
-
=-=
．
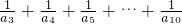故答案为30；．
分析：结合图形观察数字，发现：a3=12=3×4，a4=20=4×5，进一步得到a5=5×6；在计算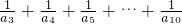的时候，根据
=-，…进行简便计算．
点评：此题考查了图形的变化规律题，注意从特殊推广到一般，能够利用分数的加减法进行简便计算．
∴a5=5×6=30．
∴
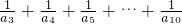=-+-+…+-=-=．故答案为30；
．分析：结合图形观察数字，发现：a3=12=3×4，a4=20=4×5，进一步得到a5=5×6；在计算
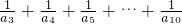的时候，根据=-，…进行简便计算．点评：此题考查了图形的变化规律题，注意从特殊推广到一般，能够利用分数的加减法进行简便计算．
练习册系列答案
相关题目
