Question

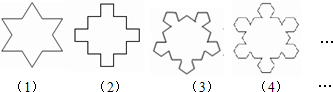
如图，第（1）个多边形由正三角形“扩展“而来，边数记为a₃，第（2）个多边形由正方形“扩展“而来，边数记为a₄，…，依此类推，由正n边形“扩展“而来的多边形的边数记为a_n（n≥3）．则a₈的值是（　　）

A．36

B．56

C．64

D．72

Answer 1

分析：首先要找出基础图形的边数与图形总边数的关系：图（1）的基础图形是三角形，边数是3，而图（1）总边数为 12，即a₃=3×4，可得规律：图形总边数=（基础图形的边数）×（基础图形的边数+1），即a_n=n×（n+1）；再由图（2）验证一下，图（2）基础图形是正方形，边数是4，而图（2）总边数为 20，即 a₄=4×5，满足规律，据此规律答题即可．

解答：解：因为图（1）总边数为 12，即a₃=3×4，图（2）基础图形是正方形，边数是4，而图（2）总边数为 20，即 a₄=4×5，…可得规律：图形总边数=（基础图形的边数）×（基础图形的边数+1），即a_n=n×（n+1）；
所以a₈=8×9=72．
故选：D．

点评：本题是一道找规律的题目，这类题型在中考中经常出现．通过观察、归纳，找出规律是关键．