题目内容
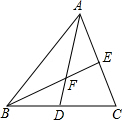如图，点D、E是△ABC的边BC、AC的中点，分别连接AD、BE相交于点F，则BE：BF=考点：平行线分线段成比例
专题：计算题
分析：作EG∥AD交BC于G，如图由EG∥AD，根据平行线分线段成比例定理得
=
，利用CE=AE可得CG=DG，再利用D点为BC的中点，易得BG：BD=3：2，然后根据平行线分线段成比例定理，由DF∥EG即可得到
=
．
| CG |
| DG |
| CE |
| AE |
| BE |
| BF |
| 3 |
| 2 |
解答：解：作EG∥AD交BC于G，如图，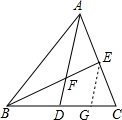
∵EG∥AD，
∴
=
，
而点E为AC的中点，
∴CE=AE，
∴CG=DG，
∵D点为BC的中点，
∴BD=CD，
∴BG：BD=3：2，
∵DF∥EG，
∴
=
=
．
故答案为3：2．
∵EG∥AD，
∴
| CG |
| DG |
| CE |
| AE |
而点E为AC的中点，
∴CE=AE，
∴CG=DG，
∵D点为BC的中点，
∴BD=CD，
∴BG：BD=3：2，
∵DF∥EG，
∴
| BE |
| BF |
| BG |
| BD |
| 3 |
| 2 |
故答案为3：2．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
相关题目
如图，在△ABC中点D是BC的中点，点E是BD的中点，AB=BD，求证：∠CAD=∠EAD．
如图，△ABC内接于⊙O，AD是⊙O的直径，∠DAC=62°，则∠ABC=正方形具有而菱形不具有的性质是（ ）
| A、对角线平分一组对角 |
| B、对角线互相垂直 |
| C、有四条对称轴 |
| D、四条边都相等 |