题目内容
(本题10分)如图所示,△ABC中,∠BAC=900,AB=AC=1,点D是BC上一个动点(不与B.C重合),在AC上取点E,使∠ADE=450.

(1)求证:△ABD∽△DEC.
(2)设BD=x,AE=y,求y关于x的函数关系式。
(3当△ADE是等腰三角形时,求AE的长。
(1)见解析;(2)y= +1;(3)AE=2-
+1;(3)AE=2- 或
或 .
.
【解析】
试题分析:(1)根据等腰直角三角可得∠ABC=∠ACB=45°,根据∠ADE=45°可得:∠BDA+∠CDE=135°
∠BDA+∠BAD=135°,∴∠BAD=∠CDE,从而得出△ABD∽△DCE;(2)根据△ABD∽△DCE,设BD=x,则CD=BC-BD= ﹣x,根据
﹣x,根据 求出CE的长度,然后根据AE=AC-CE求出函数关系式;(3)本题需要分AD=DE和ED=EA两种情况进行求解.
求出CE的长度,然后根据AE=AC-CE求出函数关系式;(3)本题需要分AD=DE和ED=EA两种情况进行求解.
试题解析:(1)证明:∵△ABC中,∠BAC=90°,AB=AC=1,∴∠ABC=∠ACB=45°.
∵∠ADE=45°,∴∠BDA+∠CDE=135°.又∠BDA+∠BAD=135°, ∴∠BAD=∠CDE. ∴△ABD∽△DCE.
(2)【解析】
∵△ABD∽△DCE, ∴ ; ∵BD=x, ∴CD=BC﹣BD=
; ∵BD=x, ∴CD=BC﹣BD= ﹣x.
﹣x.
∴ , ∴CE=
, ∴CE= x﹣
x﹣ .∴AE=AC﹣CE=1-(
.∴AE=AC﹣CE=1-( x﹣
x﹣ )=
)= ﹣
﹣ x+1.即y=
x+1.即y= ﹣
﹣ x+1.
x+1.
(3)【解析】
∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
又∵△ABD∽△DCE,∴△ABD∽△DCE.∴CD=AB=1.∴BD= ﹣1.∵BD=CE, ∴AE=AC﹣CE=2﹣
﹣1.∵BD=CE, ∴AE=AC﹣CE=2﹣ .
.
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°, ∴此时有∠DEA=90°.
即△ADE为等腰直角三角形. ∴AE=DE= AC=
AC= .AE的长为2﹣
.AE的长为2﹣ 或
或 .
.
考点:三角形相似的判定与应用、二次函数的应用.

 ;
; .
.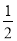 B.(- 1)2与1 C.- 1与(- 1)2 D.2与| -2|
B.(- 1)2与1 C.- 1与(- 1)2 D.2与| -2|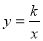 (
(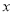 <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,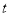 ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则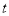 的值是( )
的值是( )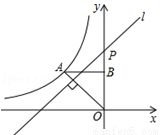
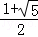 B.
B.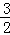 C.
C.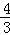 D.
D.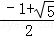
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的值为( )
的值为( )
 C.
C. D.2
D.2 的一元二次方程x2+4x+2k=0有两个实数根,求
的一元二次方程x2+4x+2k=0有两个实数根,求 的取值范围及
的取值范围及 的非负整数值.
的非负整数值. B.
B. ,3 C.6,3 D.
,3 C.6,3 D. ,
,