题目内容
7.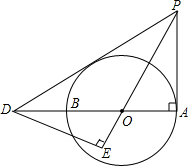 如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO
如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO(1)判断直线PD与⊙O的位置关系,并说明理由;
(2)若PA=5,AD=12,求⊙O的半径.
分析 (1)由AB是⊙O的直径,PA与⊙O相切于点A,DE⊥PO,得到∠A=∠E=90°,根据对顶角相等,得到∠DOE=∠POA,通过三角形全等,得到圆心到直线的距离等于圆的半径,得出结论;
(2)由三角形全等得出线段相等,利用勾股定理列方程求出圆的半径.
解答  解:(1)证明:∵AB是⊙O的直径,PA与⊙O相切于点A,
解:(1)证明:∵AB是⊙O的直径,PA与⊙O相切于点A,
∴∠A=90°,
∵DE⊥PO,
∴∠E=90°,
∵∠DOE=∠POA,
∴∠EDO=∠APO,
∵∠EPD=∠EDO,
∴∠APO=∠DPO,
在△AFO与△PAO中,
$\left\{\begin{array}{l}{∠PFO=∠A}\\{∠FPO=∠APO}\\{OP=OP}\end{array}\right.$,
∴△AFO≌△PAO,
∴OA=OF,
∴PD与⊙O相切;
(2)由(1)证得△AFO≌△PAO,
∴PF=PA,
∵PA=5,AD=12,
∴DP=8,AD=$\sqrt{{PA}^{2}{+AD}^{2}}$=13,
设⊙O的半径为:0A=r,
∴r2+82=(12-r)2,
∴r=$\frac{10}{3}$,
∴⊙O的半径为$\frac{10}{3}$.
点评 本题综合考查了圆周角定理,切线长定理,全等三角形的判定与性质,勾股定理的应用,能综合运用性质进行推理和计算是解此题的关键,

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.光的速度约为30万公里每秒,30万用科学记数法表示为( )
| A. | 3×105 | B. | 3×106 | C. | 3×107 | D. | 3×108 |
16. 假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
(1)小红和小慧购买西红柿数量的中位数是2,众数是2;
(2)从平均价格看,谁买的西红柿要便宜些.
小亮的说法
小明的说法
思考小亮和小明的说法,你认为谁说得对?为什么?
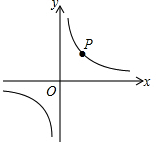
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点P(如图),点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点Q(2,5)是否在此函数图象上.
 假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:| 单价/(元/千克) | 4 | 3 | 2 | 合计 |
| 小红购买的数量/千克 | 1 | 2 | 3 | 6 |
| 小慧购买的数量/千克 | 2 | 2 | 2 | 6 |
(2)从平均价格看,谁买的西红柿要便宜些.
小亮的说法
| 每次购买单价相同,购买总量也相同,平均价格应该也一样,都是(4+3+2)÷3=3(元/千克),所以两人购买的西红柿一样便宜. |
| 购买的总量虽然相同,但小红花了16元,小慧花了18元,平均价格不一样,所以购买的西红柿便宜 |
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点P(如图),点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点Q(2,5)是否在此函数图象上.
 如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,则CD与AF的关系为相等.
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,则CD与AF的关系为相等. 如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.
如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.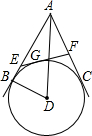 如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.
如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.