题目内容
 在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.考点:直角三角形的性质
专题:证明题
分析:根据角平分线的定义可得∠ACF=∠BCF,再根据直角三角形两锐角互余可得∠ACF+∠AFE=90°,∠BCF+∠CED=90°,然后得到∠AFE=∠CED,根据对顶角相等可得∠AEF=∠CED,从而得证.
解答:证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
点评:本题考查了直角三角形两锐角互余的性质,角平分线的定义,对顶角相等的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、-3•(-3)=-9 | ||
| B、-5-2=-3 | ||
C、2-3=-
| ||
D、3-3=
|
 已知在△ABC中,D点在AC上,E点在BC的延长线上,求证:∠ADB=∠CBD+∠CDE+∠E.
已知在△ABC中,D点在AC上,E点在BC的延长线上,求证:∠ADB=∠CBD+∠CDE+∠E. 如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.
如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.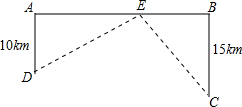 如图,高速公路上有A、B两点相距25km,C、D为两村庄.已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离和最短,最短距离的平方是多少?
如图,高速公路上有A、B两点相距25km,C、D为两村庄.已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离和最短,最短距离的平方是多少?