题目内容
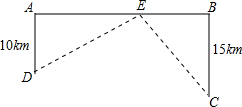如图，高速公路上有A、B两点相距25km，C、D为两村庄．已知DA=10km，CB=15km．DA⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C，D两村庄到E站的距离和最短，最短距离的平方是多少？考点：轴对称-最短路线问题
专题：
分析：根据题意构造直角三角形D′FC，再由勾股定理求解即可．
解答：
解：作D点关于AB的对称点D′，连接D′C，再作D′F⊥BC于点F，此时DE+EC最短，即求出CD′的距离即可，
∵DA=10km，CB=15km，A、B两点相距25km，
∴FC=25km，D′F=25km，
∴D′C2=FC2+D′F2=625+625=1300，
∴最短距离的平方是1300．
解：作D点关于AB的对称点D′，连接D′C，再作D′F⊥BC于点F，此时DE+EC最短，即求出CD′的距离即可，∵DA=10km，CB=15km，A、B两点相距25km，
∴FC=25km，D′F=25km，
∴D′C2=FC2+D′F2=625+625=1300，
∴最短距离的平方是1300．
点评：此题主要考查了轴对对称求最短路径以及勾股定理，得出E点位置进而构造直角三角形是解题关键．
练习册系列答案
相关题目
在△ABC中，∠BAC=90°，AD⊥BC于D，CF是∠ACB的平分线，交AD于E，交AB于F，求证：∠AEF=∠AFE．据成都新闻网报道，今年春运成都地铁运送旅客216000000人次，用科学记数法表示（ ）
| A、2.16×108人 |
| B、2.16×107人 |
| C、0.216×108人 |
| D、216×105人 |