��Ŀ����
4�� Ϊ���⽻ͨӵ�£�ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У���ͨ��ˮƽ����BCΪ8�ף���BCD=135�㣬ͨ��б��CD �ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��$\sqrt{2}$��
Ϊ���⽻ͨӵ�£�ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У���ͨ��ˮƽ����BCΪ8�ף���BCD=135�㣬ͨ��б��CD �ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��$\sqrt{2}$����1����ͨ��б��AB�ij�Ϊ3$\sqrt{6}$�ף�
��2��Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��CD���¶ȱ仺���ĺ��ͨ��б��DE���½�Ϊ30�㣬���ʱBE�ij���������������ţ�
���� ��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��������֪�ó�DM=CM=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$����AN=DM=3$\sqrt{2}$���ٽ�Rt��ANB����ͨ��б��AB���¶�i=1��$\sqrt{2}$���ó�BN=$\sqrt{2}$AN=6��Ȼ����ݹ��ɶ������AB��
��2���Ƚ�Rt��MED�����EM=$\sqrt{3}$DM=3$\sqrt{6}$���ó�EC=EM-CM=3$\sqrt{6}$-3$\sqrt{2}$���ٸ���BE=BC-EC������⣮
��� 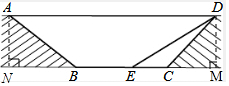 �⣺��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��
�⣺��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��
�ߡ�BCD=135�㣬
���DCM=45�㣮
����Rt��CMD�У���CMD=90�㣬CD=6��
��DM=CM=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$��
��AN=DM=3$\sqrt{2}$��
��ͨ��б��AB���¶�i=1��$\sqrt{2}$��
��tan��ABN=$\frac{AM}{BN}$=$\frac{1}{\sqrt{2}}$��
��BN=$\sqrt{2}$AN=6��
��AB=$\sqrt{A{N}^{2}+B{N}^{2}}$=3$\sqrt{6}$��
��ͨ��б��AB�ij�ԼΪ3$\sqrt{6}$�ף�
�ʴ�Ϊ��3$\sqrt{6}$��
��2������Rt��MED�У���EMD=90�㣬��DEM=30�㣬DM=3$\sqrt{2}$��
��EM=$\sqrt{3}$DM=3$\sqrt{6}$��
��EC=EM-CM=3$\sqrt{6}$-3$\sqrt{2}$��
��BE=BC-EC=8-��3$\sqrt{6}$-3$\sqrt{2}$��=8+3$\sqrt{2}$-3$\sqrt{6}$��
����ʱBE�ij�ԼΪ��8+3$\sqrt{2}$-3$\sqrt{6}$���ף�
���� ���⿼���˽�ֱ�������ε�Ӧ��-�¶��½����⣬���Ǻ����Ķ��壬���ɶ�����ȷ���������߹���ֱ���������ǽ���Ĺؼ���

 ��һ�����ǰ尴��ͼ��ʾ�ڷţ�ͼ�СϦ��Ķ����ǣ�������
��һ�����ǰ尴��ͼ��ʾ�ڷţ�ͼ�СϦ��Ķ����ǣ�������| A�� | 75�� | B�� | 90�� | C�� | 120�� | D�� | 105�� |
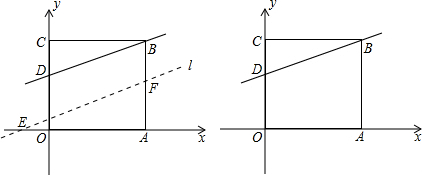




 �����M��N�������Ϸֱ��ʾʵ��m��n����������M��N����֮��ľ����ʾΪMN=m-n��m��n����n-m��m��n����|m-n|���������ν��˼�����������⣺��֪�����ϵ�A���B�ľ���Ϊ16����λ���ȣ���A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ���B�ڵ�A���Ҳ࣬��C��ʾ�������B��ʾ������Ϊ�෴��������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
�����M��N�������Ϸֱ��ʾʵ��m��n����������M��N����֮��ľ����ʾΪMN=m-n��m��n����n-m��m��n����|m-n|���������ν��˼�����������⣺��֪�����ϵ�A���B�ľ���Ϊ16����λ���ȣ���A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ���B�ڵ�A���Ҳ࣬��C��ʾ�������B��ʾ������Ϊ�෴��������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮