题目内容
【题目】已知:正方形ABCD中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
(1)当![]() 绕点
绕点![]() 旋转到
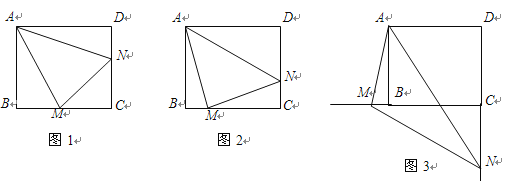
旋转到![]() 时(如图1),求证:
时(如图1),求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),则线段
时(如图2),则线段![]() 和
和![]() 之间数量关系是 ;
之间数量关系是 ;
(3)当![]() 绕点
绕点![]() 旋转到如图3的位置时,猜想线段
旋转到如图3的位置时,猜想线段![]() 和
和![]() 之间又有怎样的的数量关系呢?并对你的猜想加以说明.
之间又有怎样的的数量关系呢?并对你的猜想加以说明.
【答案】(1)见解析;
(2)BM+DN=MN;
(3)DNBM=MN,理由见解析.
【解析】
(1)延长CB至E使得BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出∠BAE=∠DAN,AE=AN,求出∠EAM=∠MAN,根据SAS证出△EAM≌△NAM,即可;
(2)证法与(1)类似,延长CB至E,使得BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出∠BAE=∠DAN,AE=AN,求出∠EAM=∠MAN,根据SAS证出△EAM≌△NAM,即可;
(3)DC上截取DE=BM,连接AE,根据SAS证△ADE≌△ABM,推出∠DAE=∠BAM,AE=AM,求出∠EAN=∠MAN.根据SAS证出△MAN≌△EAN即可.
(1)证明:如图1,延长CB至E使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,![]()
在△ADN和△ABE中
∵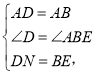
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴![]()
∵![]()
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
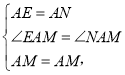
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN;
(2)线段BM,DN和MN之间数量关系是BM+DN=MN,理由如下:
延长CB至E,使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD, ![]()
在△ADN和△ABE中,
∵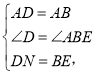
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴![]()
∵![]()
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
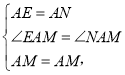
∴△EAM≌△NAM,∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN,
故答案为BM+DN=MN;
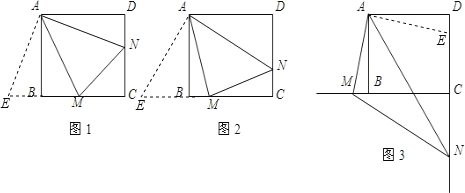 (3)DNBM=MN,理由如下:
(3)DNBM=MN,理由如下:
如图3,在DC上截取DE=BM,连接AE,
由(1)知△ADE≌△ABM(SAS),
∴∠DAE=∠BAM,AE=AM,
∴![]()
∵![]()
∴∠EAN=∠MAN.
∵在△MAN和△EAN中,
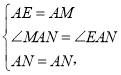
∴△MAN≌△EAN(SAS),
∴EN=MN,
即DNDE=MN,
∴DNBM=MN.

【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.