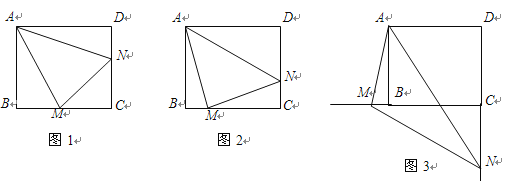
题目内容
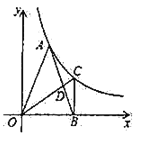
【题目】如图,![]() 为反比例函数
为反比例函数![]() (其中
(其中![]() )图象上的一点,在
)图象上的一点,在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,
,![]() .连接
.连接![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() ,交反比例函数
,交反比例函数![]() (其中
(其中![]() )的图象于点
)的图象于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,
①求线段![]() 的长;
的长;
②求线段![]() 、
、![]() 的长.
的长.
【答案】(1)12;(2)①5;②![]() ,
,![]() .
.
【解析】
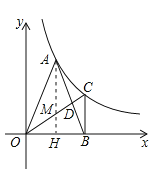
(1)过点A作AH⊥x轴,垂足为点H,AH交OC于点M,利用等腰三角形的性质可得出OH的长,利用勾股定理可得出AH的长,进而可得出点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;(2)①由OB的长,利用反比例函数图象上点的坐标特征可得出BC的长,利用勾股定理求OC的长;②由OB的长,利用反比例函数图象上点的坐标特征可得出BC的长,利用三角形中位线定理可求出MH的长,进而可得出AM的长,由AM∥BC可得出△ADM∽△BDC,利用相似三角形的性质即可求出![]() 的值,从而使问题得解.
的值,从而使问题得解.
解:(1)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() ,如图所示,
,如图所示,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() 为反比例函数
为反比例函数![]() 图象上的一点,
图象上的一点,
∴![]() .
.
(2)①∵![]() 轴,
轴,![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,则
,则![]() .
.
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴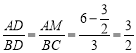 .
.
∴![]() ,
,![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目