题目内容

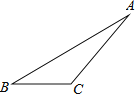
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E，延长CA交⊙O于点F．

（1）求证：DE是⊙O切线；

（2）若AB＝10cm，DE+EA＝6cm，求AF的长度．

【答案】（1）见解析；（2）.

【解析】

（1）先根据等腰三角形的性质可得，则，从而得，再根据切线判定定理即可证；

（2）如图（见解析），过点O作于点H，由题（1）可知，四边形ODEH是矩形，所以；设，则，然后在中利用勾股定理可解出x的值，从而可得AF的长度.

又，OD是半径

DE是⊙O的切线（切线判定定理）；

（2）如图，过点O作于点H，则

∴四边形ODEH是矩形

设

在中，由勾股定理得：，即

解得：或（不合题意，舍去）

又由垂径定理得：

则

故AF的长度为.

练习册系列答案
相关题目

【题目】已知：正方形ABCD中，，绕点顺时针旋转，它的两边分别交（或它们的延长线）于点．

（1）当绕点旋转到时（如图1），求证：；

（2）当绕点旋转到时（如图2），则线段和之间数量关系是 ；

（3）当绕点旋转到如图3的位置时，猜想线段和之间又有怎样的的数量关系呢？并对你的猜想加以说明．

【题目】材料一：一个正整数x能写成x=a2﹣b2（a，b均为正整数，且a≠b），则称x为“雪松数”，a，b为x的一个平方差分解，在x的所有平方差分解中，若a2+b2最大，则称a，b为x的最佳平方差分解，此时F（x）=a2+b2．

例如：24=72﹣52，24为雪松数，7和5为24的一个平方差分解，32=92﹣72，32=62﹣22，因为92+72＞62+22，所以9和7为32的最佳平方差分解，F（32）=92+72

材料二：若一个四位正整数，它的千位数字与个位数字相同，百位数字与十位数字相同，但四个数字不全相同，则称这个四位数为“南麓数”．例如4334，5665均为“南麓数”．

根据材料回答：

（1）请直接写出两个雪松数，并分别写出它们的一对平方差分解；

（2）试证明10不是雪松数；

（3）若一个数t既是“雪松数”又是“南麓数”，并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解，请求出所有满足条件的数t中F（t）的最大值．

【题目】对于二次函数y＝x2﹣3x+2和一次函数y＝﹣2x+4，把y＝t（x2﹣3x+2）+（1﹣t）（﹣2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L．现有点A（2，0）和抛物线L上的点B（﹣1，n），请完成下列任务：

（尝试）

（1）当t＝2时，抛物线y＝t（x2﹣3x+2）+（1﹣t）（﹣2x+4）的顶点坐标为　 　；

（2）判断点A是否在抛物线L上；

（3）求n的值；

（发现）

通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为　 　．

（应用）

二次函数y＝﹣3x2+5x+2是二次函数y＝x2﹣3x+2和一次函数y＝﹣2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由．

【题目】在湖心有一座小塔，小华想知道这座的高塔的高度，于是他在岸边架起了测角仪，他测量的数据如下（如图所示）：测量仪位置距水平面的距离为1.5米（即），测得塔顶的仰角为（其中），测得塔顶在水中倒影（即）的俯角为，请你根据上述数据求出这座塔的高度（即）.

【题目】在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连结BE．

（感知）如图①，过点A作AF⊥BE交BC于点F．易证△ABF≌△BCE．（不需要证明）

（探究）如图②，取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．

（1）求证：BE=FG．

（2）连结CM，若CM=1，则FG的长为　 　．

（应用）如图③，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为　 　．

【题目】如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标(0，-1)．

作出△ABC 关于原点对称的△A1B1C1，并写出点A1的坐标；

把△ABC 绕点C逆时针旋转90°，得△A2B2C2，画出△A2B2C2，并写出点A2的坐标；

(3)直接写出△A2B2C2的面积

【题目】如图是一块△ABC余料，已知AB＝20cm，BC＝7cm，AC＝15cm，现将余料裁剪成一个圆形材料，则该圆的最大面积是_____．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网