题目内容
计算题:
(1)
-
+1;
(2)
×
;
(3)(-1)-101+(π-3)0+(
)-1-
;
(4)10
-
+
.
(1)
| 12 |
| 1 | ||
2-
|
(2)
| 4 |
| 9 |
| 6 |
| 5 |
| 6 |
| 24 |
(3)(-1)-101+(π-3)0+(
| 1 |
| 2 |
(1-
|
(4)10
|
| 75 |
| 1 | ||||
|
考点:二次根式的混合运算,零指数幂,负整数指数幂
专题:计算题
分析:(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据二次很式的乘法法则运算;
(3)根据零指数幂负整数指数幂的意义和二次根式的性质运算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
(2)根据二次很式的乘法法则运算;
(3)根据零指数幂负整数指数幂的意义和二次根式的性质运算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答:解:(1)原式=2
-(2+
)+1
=2
-2-
+1
=
-1;
(2)原式=
×
×
=
;
(3)原式=-1+1+2+1-
=3-
;
(4)原式=
-5
+
-
=-4
.
| 3 |
| 3 |
=2
| 3 |
| 3 |
=
| 3 |
(2)原式=
| 4 |
| 9 |
| 5 |
| 6 |
| 6×24 |
=
| 40 |
| 9 |
(3)原式=-1+1+2+1-
| 2 |
=3-
| 2 |
(4)原式=
| 2 |
| 3 |
| 3 |
| 2 |
=-4
| 3 |
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| |||
B、
| |||
C、(-
| |||
D、
|
将方程x2+4x+2=0配方后,原方程变形为( )
| A、(x+4)2=2 |
| B、(x+2)2=2 |
| C、(x+4)2=-3 |
| D、(x+2)2=-5 |
一元二次方程kx2+2x-1=0有实数根,则k的范围是( )
| A、k≤-1 |
| B、k>-1且k≠0 |
| C、k<-1 |
| D、k≥-1且k≠0 |
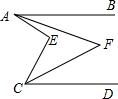 如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC=
如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC=