题目内容
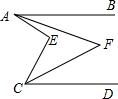 如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC=
如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC=考点:平行线的性质
专题:
分析:连接AC,先根据平行线的性质得出∠BAC+∠DCA=180°,由角平分线的定义得出∠BAF与∠DCF的度数,进而得出∠FAC+∠FCA的度数,根据三角形内角和定理即可得出结论.
解答: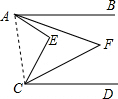 解:连接AC,
解:连接AC,
∵AB∥CD,
∴∠BAC+∠DCA=180°.
∵AF平分∠BAE,CF平分∠DCE,∠BAE=54°,∠DCE=28°,
∴∠BAF=
∠BAE=
×54°=27°,∠DCF=
∠DCE=
×28°=14°,
∴∠FAC+∠FCA=(∠BAC+∠DCA)-(∠BAF+∠DCF)=180°-(27°+14°)=139°.
∵∠FAC+∠FCA+∠AFC=180°,
∴∠AFC=180°-(∠FAC+∠FCA)=180°-139°=41°.
故答案为:41°.
 解:连接AC,
解:连接AC,∵AB∥CD,
∴∠BAC+∠DCA=180°.
∵AF平分∠BAE,CF平分∠DCE,∠BAE=54°,∠DCE=28°,
∴∠BAF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FAC+∠FCA=(∠BAC+∠DCA)-(∠BAF+∠DCF)=180°-(27°+14°)=139°.
∵∠FAC+∠FCA+∠AFC=180°,
∴∠AFC=180°-(∠FAC+∠FCA)=180°-139°=41°.
故答案为:41°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
 如图所示,直线a、b被c所截,∠1≠∠2,求证:直线a与b相交.
如图所示,直线a、b被c所截,∠1≠∠2,求证:直线a与b相交.