题目内容
如图1—49所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角 为40°,求这两座建筑
为40°,求这两座建筑 物的高.(
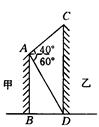
物的高.(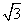 ≈1.732,ta
≈1.732,ta n 40°≈0.8391,精确到0.01 m)
n 40°≈0.8391,精确到0.01 m)
解:作AE⊥CD于E,则AE=BD=24m,在Rt△AED中,tan∠DAE= ,∴DE=AEtan 60°≈24×1.732≈41.57(m),∴AB=DE≈41.57 m.在Rt△AEC中,tan∠CAE=
,∴DE=AEtan 60°≈24×1.732≈41.57(m),∴AB=DE≈41.57 m.在Rt△AEC中,tan∠CAE= ,∴CE=AEtan 40°≈24×0.8391≈20.14(m),∴CD=CE+DE≈20.14+41.57=61.71(m),∴甲建筑物的高AB约为41.57 m,乙建筑物的高CD约为61.7l m.
,∴CE=AEtan 40°≈24×0.8391≈20.14(m),∴CD=CE+DE≈20.14+41.57=61.71(m),∴甲建筑物的高AB约为41.57 m,乙建筑物的高CD约为61.7l m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ∠B都是锐角,且 sin A=
∠B都是锐角,且 sin A= ,cos B=
,cos B= ,则△ABC三个角的大小关系是( )
,则△ABC三个角的大小关系是( ) 中,
中, ,
, ,则
,则 .
. ,则tanB等于( )
,则tanB等于( ) B.
B. C
C .
.
 D.
D.

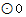 的直径,点D在
的直径,点D在
 -5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( )
-5x+6=0的两根,两圆的圆心距为1,则两圆的位置关系是( ) (
( )的图象如图,关于该二次函数,下列说法错误的是( )
)的图象如图,关于该二次函数,下列说法错误的是( )

 ,y随x的增大而减小 D.当
,y随x的增大而减小 D.当 时,
时,