题目内容
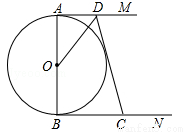
(9分)如图,AB是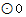 的直径,点D在
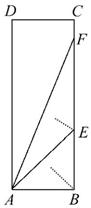
的直径,点D在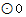 上,∠DAB=45°,BC∥AD,CD∥AB.
上,∠DAB=45°,BC∥AD,CD∥AB.
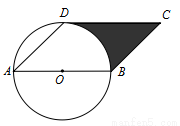
(1)、判断直线CD与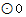 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)、若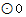 的半径为1,求图中阴影部分的面积(结果保留π).
的半径为1,求图中阴影部分的面积(结果保留π).
(1)、相切;(2)、 .
.
【解析】
试题分析:(1)、连接OD,根据OA=OD,∠ODA=45°得出∠AOD=90°,根据CD∥AB得出∠ODC=90°,从而说明切线;(2)、首先求出梯形OBCD的面积,然后利用梯形的面积减去扇形OBD的面积求出阴影部分的面积.
试题解析:(1)直线CD与⊙O相切. 理由如下:
连接OD. ∵OA=OD,∠DAB=45°,∴∠ODA=45°.
∴∠AOD=90°. 又∵CD∥AB, ∴∠ODC=∠AOD=90°,即OD⊥CD.
又∵点D在⊙O上, ∴直线CD与⊙O相切.
(2)、∵BC∥AD,CD∥AB, ∴ 四边形ABCD是平行四边形.∴CD=AB=2.
∴梯形OBCD的面积=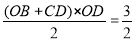
∴图中阴影部分的面积=梯形OBCD的面积-扇形OBD的面积=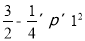 =
=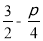 .
.
考点:切线的判定、扇形的面积计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 n30°-3 tan 45°+4 cos 6
n30°-3 tan 45°+4 cos 6 为40°,求这两座建筑
为40°,求这两座建筑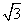 ≈1.732,ta
≈1.732,ta n 40°≈0.8391,精确到0.01 m)
n 40°≈0.8391,精确到0.01 m)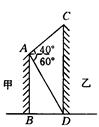
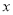 的方程为
的方程为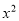 +(m+2)x+2m-1=0.
+(m+2)x+2m-1=0.