题目内容
13.已知x,y满足方程组$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$,(1)用x的代数式表示y;
(2)若不论x取何值,代数式(kx-y)(y+$\frac{1}{2}$x)的值都为常数,求此时k的值以及该代数式的值.
分析 (1)方程组两方程变形后,得到一个二元一次方程,用x表示出y即可;
(2)把表示出的y代入原式,利用多项式乘以多项式法则化简,根据代数式值为常数确定出k的值,以及此时代数式的值即可.
解答 解:(1)$\left\{\begin{array}{l}{x+3y=4-a①}\\{x-y=3a②}\end{array}\right.$,
将①式左右两边都乘3得,3x+9y=12-3a③,
②+③,得4x+8y=12,即y=-$\frac{1}{2}$x+$\frac{3}{2}$;
(2)(kx-y)(y+$\frac{1}{2}$x)=(kx+$\frac{1}{2}$x-$\frac{3}{2}$)(-$\frac{1}{2}$x+$\frac{3}{2}$+$\frac{1}{2}$x)=$\frac{3}{2}$[(k+$\frac{1}{2}$)x-$\frac{3}{2}$],
当k=-$\frac{1}{2}$时,无论x取何值,代数式(kx-y)(y+$\frac{1}{2}$x)的值都为常数-$\frac{9}{4}$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.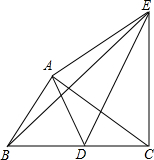 如图,将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置,使B点的对应点D落在BC边上,连接EB、EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③∠BED=30°;④ED=2AB.其中正确的是( )
如图,将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置,使B点的对应点D落在BC边上,连接EB、EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③∠BED=30°;④ED=2AB.其中正确的是( )
 如图,将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置,使B点的对应点D落在BC边上,连接EB、EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③∠BED=30°;④ED=2AB.其中正确的是( )
如图,将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置,使B点的对应点D落在BC边上,连接EB、EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③∠BED=30°;④ED=2AB.其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
18.某省参加学业考试的同学约有10万人,若女生约有a万人,则男生约有( )
| A. | (10-a)万人 | B. | (10+a)万人 | C. | 10a万人 | D. | $\frac{10}{a}$万人 |
3.$\sqrt{(a-b)^{2}}$+$\root{5}{(a-b)^{5}}$的值是( )
| A. | 0 | B. | 2(a-b) | C. | 0或2(a-b) | D. | a-b |
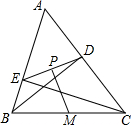 如图,BD和CE是△ABC的高,点M为BC的中点,连接DE,过点M作DE的垂线,垂足为点P.若PM=5,DE=6,tan∠DBC=$\frac{{\sqrt{2}}}{2}$,则CD的长为$\frac{2\sqrt{102}}{3}$.
如图,BD和CE是△ABC的高,点M为BC的中点,连接DE,过点M作DE的垂线,垂足为点P.若PM=5,DE=6,tan∠DBC=$\frac{{\sqrt{2}}}{2}$,则CD的长为$\frac{2\sqrt{102}}{3}$. 已知:如图,AB=AC,BD⊥AC于D,CE⊥AB于E.欲证明BD=CE,需证明△BDC≌△CEB,理由为
已知:如图,AB=AC,BD⊥AC于D,CE⊥AB于E.欲证明BD=CE,需证明△BDC≌△CEB,理由为