题目内容
12．
如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，下列结论一定成立的是（ ）| A． | ∠A=∠1+∠2 | B． | 2∠A=∠1+∠2 | C． | 3∠A=2∠1+∠2 | D． | 3∠A=2（∠1+∠2） |
分析 延长BE、CD相交与点A′，四边形的内角和为360°及翻折的性质，就可求出2∠A=∠1+∠2这一始终保持不变的性质．
解答 解：延长BE、CD相交与点A′．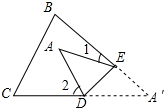
∵在四边形ADA′E中，∠A+∠A′+∠ADA′+∠AEA′=360°，
∴2∠A+180°-∠2+180°-∠1=360°，
∴2∠A=∠1+∠2．
故选：B．
点评 本题主要考查的是翻折变换、四边形的内角和是360°，掌握此类辅助线的作法是解题的关键．
练习册系列答案
全程金卷系列答案
快乐5加2金卷系列答案
相关题目
中，字母x的取值范围是（ ）
B. 
C. 
D. 
如图，将BM′绕点O按逆时针方向旋转45°后得到△A′OB′，若△AOB=15°，则∠AOB′的度数是30°．
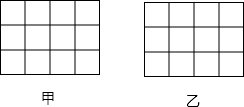如图，正方形网格中的每个小正方形=边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图．
如图，将△ABC绕点B顺时针旋转40°得到△DBE，若此时点A的对应点D恰好落在边AC上，且∠ABE=90°，则∠C的度数为60°．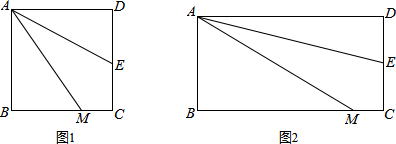
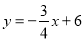与
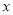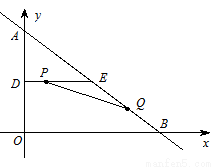
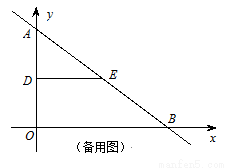
轴、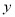
轴分别交于点B、 A，点D、E分别是AO、AB的中点，连接DE，点P从点D出发，沿DE方向匀速运动，速度为1cm/s；与此同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为
.
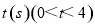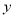（cm2），求y与t之间的函数关系式；
1．tan45°的值等于（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |