题目内容
 如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数.
如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数.考点:角平分线的定义
专题:
分析:由OD平分∠AOC和∠BOC=4∠AOD,可求出∠AOC=60°,再求出∠COB的度数,即可求出∠BOD,利用∠COE=∠DOE-∠COD即可求出.
解答:解:∵OD平分∠AOC,
∴∠AOD=∠COD=
∠AOC,
∵∠BOC=4∠AOD,
∴∠BOC=2∠AOC,
∵∠BOC+∠AOC=180°,
∴3∠AOC=180°,
∴∠AOC=60°,
∴∠COD=
∠AOC=30°,∠BOC=2∠AOC=120°
∴∠BOD=150°,
∵OE平分∠BOD,
∴∠EOD=∠BOE=75°,
∴∠COE=∠DOE-∠COD=75°-30°=45°.
∴∠AOD=∠COD=
| 1 |
| 2 |
∵∠BOC=4∠AOD,
∴∠BOC=2∠AOC,
∵∠BOC+∠AOC=180°,
∴3∠AOC=180°,
∴∠AOC=60°,
∴∠COD=
| 1 |
| 2 |
∴∠BOD=150°,
∵OE平分∠BOD,
∴∠EOD=∠BOE=75°,
∴∠COE=∠DOE-∠COD=75°-30°=45°.
点评:本题主要考查了角平分线的定义,解题的关键是利用角平分线的定义找出各角之间的关系.

练习册系列答案
相关题目
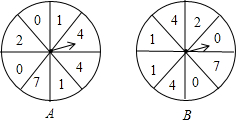 北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下:
北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下: