题目内容
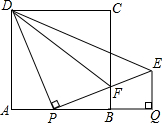 如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:
分析:(1)由题意得:PD=PE,∠DPE=90°,又由正方形ABCD的边长为1,易证得△ADP≌△QPE,然后由全等三角形的性质,求得线段PQ的长;
(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.
(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.
解答:解:(1)根据题意得:PD=PE,∠DPE=90°,
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
,
∴△ADP≌△QPE(AAS),
∴PQ=AD=1;
(2)∵△PFD∽△BFP,
∴
=
,
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴
=
,
∴
=
,
∴PA=PB,
∴PA=
AB=
∴当PA=
时,△PFD∽△BFP.
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
|
∴△ADP≌△QPE(AAS),
∴PQ=AD=1;
(2)∵△PFD∽△BFP,

∴
| PB |
| BF |
| PD |
| PF |
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴
| PD |
| PF |
| AP |
| BF |
∴
| AP |
| BF |
| PB |
| BF |
∴PA=PB,
∴PA=
| 1 |
| 2 |
| 1 |
| 2 |
∴当PA=
| 1 |
| 2 |
点评:此题考查了相似三角形的判定与性质、正方形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果a>b,那么下列不等式中不成立的是( )
| A、a-3>b-3 | ||||
B、
| ||||
| C、-a<-b | ||||
| D、-3a>-3b |
在?ABCD中,∠A:∠B:=2:3,则∠D=( )
| A、36° | B、108° |
| C、72° | D、60° |
 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E. 如图所示的两幅不完全的统计图表:
如图所示的两幅不完全的统计图表: