题目内容
5.利用图形面积可以证明乘法公式,也可以解释代数中恒等式的正确性.(1)首先请同学们观察用硬纸片拼成的图形(如图1),根据图形的面积,写出它能说明的乘法公式(a+b)2=a2+2ab+b2;
(2)请同学们观察用硬纸片拼成的图形(如图2),根据图形的面积关系,写出一个代数恒等式.
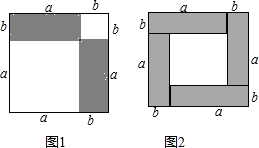
分析 (1)图中可以得出,大正方形的边长为a+b,大正方形的面积就为(a+b)2,2个矩形的边长相同,且长为a,宽为b,则2个矩形的面积为2ab,空白的是两个正方形,较大的正方形的边长为a,面积等于a2,小的正方形边长为b,面积等于b2,大正方形面积减去2个阴影矩形的面积就等于空白部分的面积.
(2)图中可以得出,大正方形的边长为a+b,大正方形的面积就为(a+b)2,4个矩形的边长相同,且长为a,宽为b,则4个矩形的面积为4ab,中间空心的正方形的边长为a-b,面积等于(a-b)2,大正方形面积减去4个阴影矩形的面积就等于中间空白部分的面积.
解答 解:(1)∵阴影部分都是全等的矩形,且长为a,宽为b,
∴2个矩形的面积为2ab,
∵大正方形的边长为a+b,
∴大正方形面积为(a+b)2,
∴空白正方形的面积为a2和b2,
∴(a+b)2=a2+2ab+b2.
故答案为(a+b)2=a2+2ab+b2.
(2)∵四周阴影部分都是全等的矩形,且长为a,宽为b,
∴四个矩形的面积为4ab,
∵大正方形的边长为a+b,
∴大正方形面积为(a+b)2,
∴中间小正方形的面积为(a+b)2-4ab,
∵中间小正方形的面积也可表示为:(a-b)2,
∴(a-b)2=(a+b)2-4ab.
点评 本题考查了完全平方公式的几何意义,用不同的方法表示相应的面积是解题的关键.

练习册系列答案
相关题目
20. 如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
 如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
19.计算a6•a2的结果是( )
| A. | a4 | B. | a8 | C. | a12 | D. | a3 |

 如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.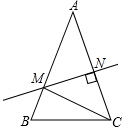 如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°.
如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°.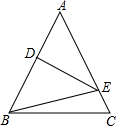 如图△ABC中,AB=AC,DE⊥AB,D是AB的中点,DE交AC于E点,连结BE,BC=10cm,
如图△ABC中,AB=AC,DE⊥AB,D是AB的中点,DE交AC于E点,连结BE,BC=10cm, 列方程解应用题.
列方程解应用题.