题目内容
 要测量不能到达的两个目标A、B间的距离,一种测量方法如下:
要测量不能到达的两个目标A、B间的距离,一种测量方法如下:(1)选择两个观测点C、D,测出它的之间的距离,并按一定的比例尺将它们画在纸上;
(2)在点C测出∠ADC和∠BDC的度数,在纸上画出点A、B(如图),这样,量出A、B两点间的图上距离,就可以根据比例尺求出A、B两点间的实际距离.
若测得CD=300m,∠ACD=45°,∠BCD=75°,∠ADC=80°,∠BDC=54°,请用1:5000的比例尺在纸上分别画出点C、D和点A、B,并通过度量A、B两点间的图上距离求出A、B两点间的实际距离.
考点:相似三角形的应用
专题:
分析:(1)根据比例尺求出CD的图上距离为6cm,然后分别作出∠ACD=45°,∠BCD=75°,∠ADC=80°,∠BDC=54°,即可得到点A、B的位置;
(2)测量出AB的图上距离为3.6cm,然后根据比例尺列出算式求解即可.
(2)测量出AB的图上距离为3.6cm,然后根据比例尺列出算式求解即可.
解答: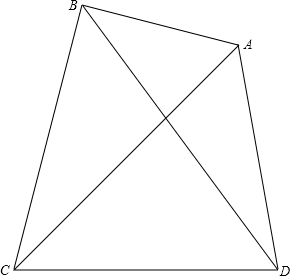 解:(1)300m=30000cm,
解:(1)300m=30000cm,
∵比例尺为1:5000,
∴CD:30000=1:5000,
解得CD=6cm,
画出平面图形如图所示;
(2)经测量AB=3.6cm,设AB的实际距离为xm,
由题意得,3.6:x=6:30000,
解得x=180m.
答:A、B两点间的实际距离为180m.
 解:(1)300m=30000cm,
解:(1)300m=30000cm,∵比例尺为1:5000,
∴CD:30000=1:5000,
解得CD=6cm,
画出平面图形如图所示;
(2)经测量AB=3.6cm,设AB的实际距离为xm,
由题意得,3.6:x=6:30000,
解得x=180m.
答:A、B两点间的实际距离为180m.
点评:本题考查了相似三角形的应用,主要利用了比例尺的定义,难点在于准确作出图形并测量出AB的图上距离.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
已知抛物线y=ax2+bx+c,经过A(4,0),B(12,0)两点,那么它的对称轴是( )
| A、直线x=7 | B、直线x=8 |
| C、直线x=9 | D、无法确定 |
 如图,在四边形PMNO中,MO⊥ON,各边的长度在图上已标出,求证:四边形PMON是平行四边形.
如图,在四边形PMNO中,MO⊥ON,各边的长度在图上已标出,求证:四边形PMON是平行四边形. 如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于M、N.
如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于M、N. 如图所示,矩形ABCD的对角线AC、BD相交于点O,BE平分∠ABC,交AC于点E,交CD于点F,且∠OBF=15°,求证:OF=EF.
如图所示,矩形ABCD的对角线AC、BD相交于点O,BE平分∠ABC,交AC于点E,交CD于点F,且∠OBF=15°,求证:OF=EF.