题目内容
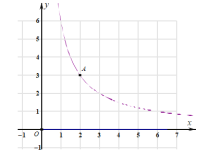
【题目】如图,在平面直角坐标系 xOy中,反比例函数 y ![]() x 0 的图象经过点 A2,3 ,直线y ax , y
x 0 的图象经过点 A2,3 ,直线y ax , y ![]() 与反比例函数 y
与反比例函数 y ![]() x 0 分别交于点 B,C两点.
x 0 分别交于点 B,C两点.
(1)直接写出 k 的值 ;
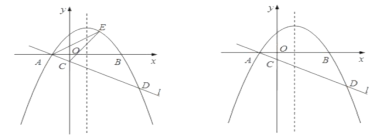
(2)由线段 OB,OC和函数 y ![]() x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
① 当 A点与 B点重合时,直接写出区域 W 内的整点个数 ;
② 若区域 W内恰有 8个整点,结合函数图象,直接写出 a的取值范围 .
【答案】(1)6;(2)①2;②![]() .
.
【解析】
(1)将点A代入y ![]() 可得
可得![]() 值;
值;
()①由A点与 B点重合可知B点坐标,代入![]() 可得
可得![]() 值,易知y
值,易知y ![]() 与点C坐标,画出图像即可确定区域 W 内的整点个数;
与点C坐标,画出图像即可确定区域 W 内的整点个数;
②确定区域内的8个整点,画出函数图像,由此可确定a的取值范围.
解:(1)将点![]() 代入y
代入y ![]() 得
得![]() ,解得
,解得![]() ,
,
所以k 的值为6;
(2)①由A点与 B点重合可知B点坐标为![]() ,代入
,代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]() ,
,
联立 ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
将![]() 代入
代入![]() 得
得![]() ,
,
![]()
画出图像,如图所示,

由图像可得区域 W 内的整点为![]() ,其个数为2个;
,其个数为2个;
②如图所示,8个整点为![]() ,
,
当![]() 过点
过点![]() 时,
时,![]() ,
,
当![]() 过点
过点![]() 时,
时,![]() ,
,
由图像可得![]() 时,区域 W内恰有 8个整点.
时,区域 W内恰有 8个整点.


 第1卷单元月考期中期末系列答案
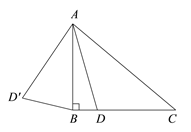
第1卷单元月考期中期末系列答案【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.