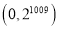��Ŀ����
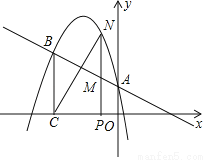
��ͼ��ʾ�����κ���y=ax2��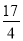 x+c��ͼ����A��0��1����B����3��
x+c��ͼ����A��0��1����B����3�� 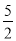 ����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C��
����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C��
��1����ֱ��AB�Ľ���ʽ�Ͷ��κ����Ľ���ʽ��
��2����N�Ƕ��κ���ͼ����һ�㣨��N��AB�Ϸ�������N��NP��x�ᣬ����Ϊ��P����AB�ڵ�M����MN�����ֵ��
��3����N�Ƕ��κ���ͼ����һ�㣨��N��AB�Ϸ������Ƿ���ڵ�N��ʹ��BM��NC���ֱƽ�֣������ڣ������������������N������ꣻ�������ڣ�˵�����ɣ�
��ϰ��ϵ�д�
�����Ŀ
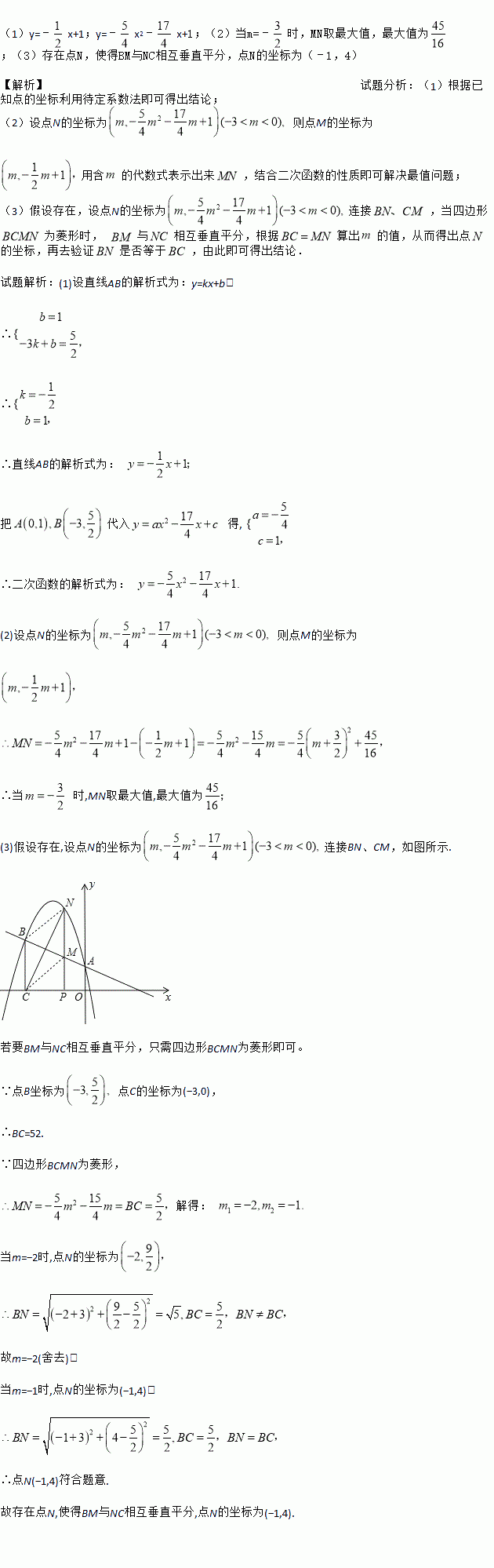

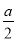 x3y|b��3|�ǹ���x��y�ĵ���ʽ����ϵ��Ϊ
x3y|b��3|�ǹ���x��y�ĵ���ʽ����ϵ��Ϊ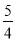 �� ������4����a��b��ֵ��
�� ������4����a��b��ֵ��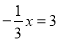 ����x=-1�� �ܴ�
����x=-1�� �ܴ�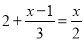 ����6+2(x-1)=3x.
����6+2(x-1)=3x.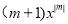 +3=0�ǹ���x��һԪһ�η��̣���m��ֵ�� ��
+3=0�ǹ���x��һԪһ�η��̣���m��ֵ�� ��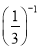 +16�£���2��3+��2005���У�0��
+16�£���2��3+��2005���У�0��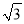 tan30��
tan30��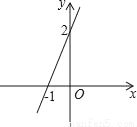
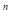 y
y �� -
�� - xy
xy ��ͬ�����m + n =__________.
��ͬ�����m + n =__________.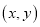 ��һ�β����任��Ϊ
��һ�β����任��Ϊ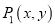 ��������任�������£�
��������任�������£�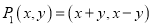 ���ҹ涨
���ҹ涨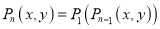 ��
��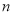 ����
����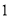 ����������
����������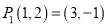 ��
�� 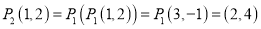 ��
�� 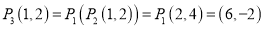 ��
��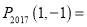 �� ����
�� ����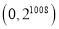 B.
B. 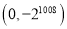 C.
C. 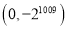 D.
D.