题目内容
如图,在△ABC中,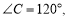
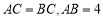 ,半圆的圆心O在AB上,且与AC,BC分别相切于点D, E.
,半圆的圆心O在AB上,且与AC,BC分别相切于点D, E.

(1)求半圆O的半径;
(2)求图中阴影部分的面积.
(1)1;(2)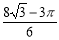 .
.
【解析】
试题分析:(1)连接OC,OD,OE,根据切线的性质得到OD⊥AC,在直角△AOD中,用30°角所对的直角边等于斜边的一半,可以求出半圆的半径.
(2)先在直角△AOC中求出OC的长,计算出△ABC的面积,然后用三角形的面积减去半圆的面积得到阴影部分的面积.
试题解析:(1)【解析】
连结OD, OC,
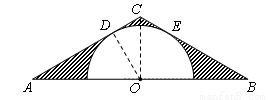
∵半圆与AC,BC分别相切于点D,E
∴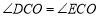 ,且
,且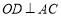
∵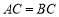 ,
,
∴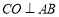 且O是AB的中点
且O是AB的中点
∴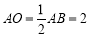
∵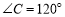 ,∴
,∴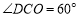
∴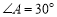
∴在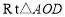 中,
中,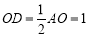
即半圆的半径为1.
(2)设CO=x,则在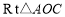 中,因为
中,因为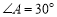 ,所以AC=2x,由勾股定理得:
,所以AC=2x,由勾股定理得:
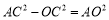
即 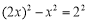
解得 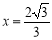 (
(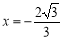 舍去)
舍去)
∴ 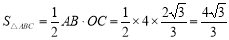 .
.
∵ 半圆的半径为1,
∴ 半圆的面积为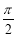 ,
,
∴ 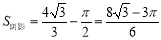 .
.
考点:1.扇形面积的计算;2.切线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

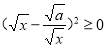 ,所以
,所以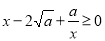 ,从而
,从而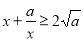 (当x=
(当x=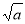 时取等号).记函数
时取等号).记函数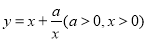 ,由上述结论可知:当x=
,由上述结论可知:当x=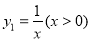 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为 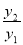 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.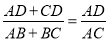 B.
B.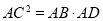
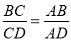 D.
D.
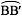 的长为( )
的长为( )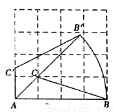
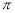 B.
B.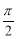 C.7
C.7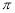 D.6
D.6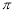
 B.
B.  C.
C.  D.
D. 


