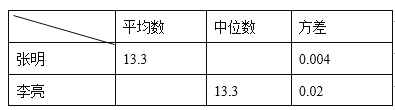
题目内容
【题目】“综合与实践”是以问题为中心,以活动为平台,以解决某一实际的数学问题为目标,综合应用知识和方法解决问题,它是对数学知识的延伸和发展,是对理解、运用数学基础知识和基本技能的升华过程.请同学们运用你所学的数学知识来研究和解决以下问题吧.
(1)探究:已知![]() 是平面上一个运动的点,若
是平面上一个运动的点,若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;若
的长最小,最小值为 ;若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;
的长最小,最小值为 ;
(2)应用:已知![]() 是一运动的点,
是一运动的点,![]() ,
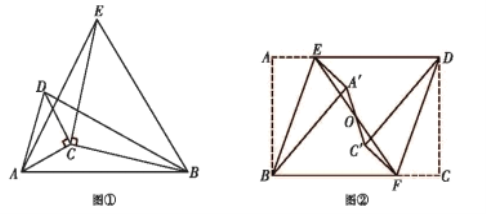
,![]() ,如图①所示,分别以
,如图①所示,分别以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,且
,且![]() ,连接
,连接![]() 和
和![]() .
.
①在图中找出与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②何时线段![]() 可以取得最小值?请直接写出线段
可以取得最小值?请直接写出线段![]() 的最小值;
的最小值;
(3)拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() 并延长与
并延长与![]() 边交于点
边交于点![]() ,现将图中
,现将图中![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 分别落在矩形
分别落在矩形![]() 内的点
内的点![]() ,
,![]() 处,连接
处,连接![]() ,则
,则![]() 的长有最小值吗?若有,请直接写出
的长有最小值吗?若有,请直接写出![]() 的长的最小值;若没有,请说明理由.
的长的最小值;若没有,请说明理由.
【答案】(1)线段![]() 上,2;线段
上,2;线段![]() 的延长线上,2;(2)①
的延长线上,2;(2)①![]() ,理由见详解;②当点C在AB上时,AE的值最小,最小值为
,理由见详解;②当点C在AB上时,AE的值最小,最小值为![]() ;(3)有最小值,最小值为
;(3)有最小值,最小值为![]() .
.
【解析】
(1)由题意可知,当点![]() 位于线段
位于线段![]() 上时有最小值,根据AB和PA的长确定点P是在线段
上时有最小值,根据AB和PA的长确定点P是在线段![]() 上还是在
上还是在![]() 的延长线上即可;
的延长线上即可;
(2)①证明![]() 全等即可找出与AD相等的线段;
全等即可找出与AD相等的线段;
②由(1)的结论,举一反三,即可找出AE取最小值的情况,再计算即可;
(3)根据前两问的启发,找到![]() 取最小值的情况,再推理计算即可.
取最小值的情况,再推理计算即可.
(1)由题意可得,当![]() ,
,![]() 时,当点
时,当点![]() 位于线段
位于线段![]() 上时,线段
上时,线段![]() 的长最小,最小值为2;
的长最小,最小值为2;
当![]() ,
,![]() 时,当点
时,当点![]() 位于线段
位于线段![]() 的延长线上时,线段
的延长线上时,线段![]() 的长最小,最小值为2;
的长最小,最小值为2;
(2)①![]()
理由:![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() ,
,![]()
![]()
![]()
![]() ;
;
②当点C在AB上时,AE的值最小,
此时C,D,E三点共线,CE⊥AB,
∴在Rt△ACE中,![]() ,
,
∵AB=3,AC=1,
∴BC=2,
∵![]() ,
,
∴CE=2,
∴![]() ,
,
∴最小值为![]() ;
;
(3)有最小值,
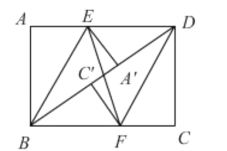
如图,要使![]() 最小,只有点
最小,只有点![]() ,
,![]() 落在矩形对角线BD上,
落在矩形对角线BD上,
矩形的对角线![]() ,
,
由对折可得![]() =BA=4,
=BA=4,
∴![]() =BD-
=BD-![]() =
=![]() -4,
-4,
∵四边形ABCD是矩形,且点![]() ,
,![]() 落在矩形对角线BD上,
落在矩形对角线BD上,
∴根据翻折的性质和矩形的性质可得,![]() =
=![]() ,∠
,∠![]() =∠
=∠![]() ,∠EDB=∠FBD,
,∠EDB=∠FBD,
∴△![]() ≌△
≌△![]() (AAS),
(AAS),
∴![]() =
=![]() ,
,
∴![]() =BD-
=BD-![]() -
-![]() =
=![]() -2(
-2(![]() -4)=
-4)=![]() ,
,
∴![]() 长的最小值为
长的最小值为![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案