Question

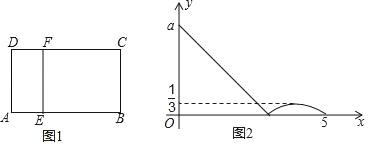
【题目】如图1，在矩形ABCD中，动点E从A出发，沿A→B→C方向运动，当点E到达点C时停止运动，过点E作EF⊥AE交CD于点F，设点E运动路程为x，CF=y，如图2所表示的是y与x的函数关系的大致图象，给出下列结论：①a=3；②当CF=时，点E的运动路程为或或，则下列判断正确的是（　　）

A. ①②都对 B. ①②都错 C. ①对②错 D. ①错②对

Answer 1

【答案】A

【解析】

由已知，AB=a，AB+BC=5，当E在BC上时，如图，可得△ABE∽△ECF，继而根据相似三角形的性质可得y=﹣，根据二次函数的性质可得﹣，由此可得a=3，继而可得y=﹣，把y=代入解方程可求得x1=，x2=，由此可求得当E在AB上时，y=时，x=，据此即可作出判断.

由已知，AB=a，AB+BC=5，

当E在BC上时，如图，

∵E作EF⊥AE，

∴△ABE∽△ECF，

∴，

∴，

∴y=﹣，

∴当x=时，﹣，

解得a1=3，a2=（舍去），

∴y=﹣，

当y=时，=﹣，

解得x1=，x2=，

当E在AB上时，y=时，

x=3﹣=，

故①②正确，

故选A．