题目内容
已知函数y=(m+1)xm2-3是正比例函数，且图象在第二、四象限内，则m的值是 ．
考点：正比例函数的定义
专题：
分析：当一次函数的图象经过二、四象限可得其比例系数为负数，据此求解．
解答：解：∵函数y=(m+1)xm2-3是正比例函数，
∴m2-3=1且m+1≠0，
解得 m=±2．
又∵函数图象经过第二、四象限，
∴m+1＜0，
解得 m＜-1，
∴m=-2．
故答案是：-2．
∴m2-3=1且m+1≠0，
解得 m=±2．
又∵函数图象经过第二、四象限，
∴m+1＜0，
解得 m＜-1，
∴m=-2．
故答案是：-2．
点评：此题主要考查了正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图，在△ABC中，∠A=65°，∠B=45°，BC的垂直平分线分别交AB、BC于D、E，则∠ACD=已知△ABC，求作一点P，使P到三角形三边的距离相等，则点P是（ ）
| A、三边中垂线的交点 |
| B、三边的高线的交点 |
| C、三边中线的交点 |
| D、三个内角的角平分线的交点 |
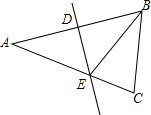如图，AB=AC，AB的垂直平分线交AB于D，交AC于E，BE恰好平分∠ABC，有以下结论：