Question

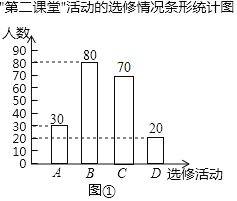
【题目】某学校为了解学生“第二课堂“活动的选修情况，对报名参加A．跆拳道，B．声乐，C．足球，D．古典舞这四项选修活动的学生（每人必选且只能选修一项）进行抽样调查．并根据收集的数据绘制了图①和图②两幅不完整的统计图．

根据图中提供的信息，解答下列问题：

（1）本次调查的学生共有　 人；在扇形统计图中，B所对应的扇形的圆心角的度数是　 　；

（2）将条形统计图补充完整；

（3）在被调查选修古典舞的学生中有4名团员，其中有1名男生和3名女生，学校想从这4人中任选2人进行古典舞表演．请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率．

Answer 1

【答案】（1）200、144；（2）补全图形见解析；（3）被选中的2人恰好是1男1女的概率．

【解析】

（1）由A活动的人数及其所占百分比可得总人数，用360°乘以B活动人数所占比例即可得；
（2）用总人数减去其它活动人数求出C的人数，从而补全图形；
（3）列表得出所有等可能的情况数，找出刚好抽到一男一女的情况数，即可求出所求的概率．

（1）本次调查的学生共有30÷15%＝200（人），

扇形统计图中，B所对应的扇形的圆心角的度数是360°× ＝144°，

故答案为：200、144；

（2）C活动人数为200﹣（30+80+20）＝70（人），

补全图形如下：

（3）画树状图为：

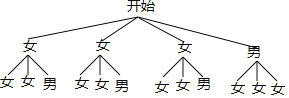
或列表如下：

	男	女1	女2	女3
男	﹣﹣﹣	（女，男）	（女，男）	（女，男）
女1	（男，女）	﹣﹣﹣	（女，女）	（女，女）
女2	（男，女）	（女，女）	﹣﹣﹣	（女，女）
女3	（男，女）	（女，女）	（女，女）	﹣﹣﹣

∵共有12种等可能情况，1男1女有6种情况，

∴被选中的2人恰好是1男1女的概率．