题目内容
10.化简:$\frac{m}{m-n}$+$\frac{2nm}{(m+n)(m-n)}$-$\frac{n(m-n)}{m+n}$.分析 原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:原式=$\frac{m(m+n)+2mn-n(m-n)^{2}}{(m+n)(m-n)}$=$\frac{{{m}^{2}+n}^{3}+2mn}{{m}^{2}-{n}^{2}}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
20.已知三条线段的长是1,$\sqrt{2}$,2,请你再添上一条线段,使这四条线段成比例线段,则这条线段长为2$\sqrt{2}$或$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
15. 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )| A. | $\left\{\begin{array}{l}{x>4}\\{x≤-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<4}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>4}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤4}\\{x>-1}\end{array}\right.$ |
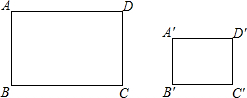 如图所示,有矩形ABCD和矩形A′B′C′D′,AB=8cm,BC=12cm,A′B′=4cm,B′C′=6cm.
如图所示,有矩形ABCD和矩形A′B′C′D′,AB=8cm,BC=12cm,A′B′=4cm,B′C′=6cm.