��Ŀ����
������y��ax2��bx��c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵������ȷ����___________ (��д���)��
����������x���һ������Ϊ(3��0)���ں���y��ax2��bx��c�����ֵΪ6���������ߵĶԳ�����x��0.5�����ڶԳ�����࣬y��x�����������
 �٢ۢ�
������������ͼ��,��x=-2,y=0,���������ߵĶԳ���,��x=3ʱ,y=0,����������x��Ľ���Ϊ(-2,0)��(3,0);
�������ߵĶԳ�����ֱ��x=3-,
���ݱ������ݵõ������ߵĿ�������,
�൱x=ʱ,���������ֵ,������x=0,��1��Ӧ�ĺ���ֵ6,
������ֱ��x=�����,y��x���������.
���Ԣ٢ۢ���ȷ,�ڴ�.
�ʴ�Ϊ:�٢ۢ�.
�٢ۢ�
������������ͼ��,��x=-2,y=0,���������ߵĶԳ���,��x=3ʱ,y=0,����������x��Ľ���Ϊ(-2,0)��(3,0);
�������ߵĶԳ�����ֱ��x=3-,
���ݱ������ݵõ������ߵĿ�������,
�൱x=ʱ,���������ֵ,������x=0,��1��Ӧ�ĺ���ֵ6,
������ֱ��x=�����,y��x���������.
���Ԣ٢ۢ���ȷ,�ڴ�.
�ʴ�Ϊ:�٢ۢ�.
 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�����˵���д������( )
A ���ں���y����x2�У���x��0ʱy�����ֵ0
B���ں���y��2x2�У���x��0ʱy��x�����������
C��������y��2x2��y����x2��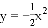 �У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
�У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
D������a���������Ǹ�����������y��ax2�Ķ��㶼������ԭ��
 C
���������ɺ����Ľ���ʽy����x2����֪a=-1��0���õ������Ŀ������£������ֵy=0����A��ȷ��
�ɺ����Ľ���ʽy��2x2����֪��Գ���Ϊy�ᣬ�Գ������ߣ�x��0����y��x�������С���Գ�����ұߣ�x��0����y��x���������B��ȷ��
���ݶ��κ��������ʣ���֪ϵ��a�������ڷ���Ϳ��ڴ�С����a��ֵԽ��ԽС����֪������y��2x2�Ŀ�����С��������y����x2�Ŀ��ڵڶ�С...
C
���������ɺ����Ľ���ʽy����x2����֪a=-1��0���õ������Ŀ������£������ֵy=0����A��ȷ��
�ɺ����Ľ���ʽy��2x2����֪��Գ���Ϊy�ᣬ�Գ������ߣ�x��0����y��x�������С���Գ�����ұߣ�x��0����y��x���������B��ȷ��
���ݶ��κ��������ʣ���֪ϵ��a�������ڷ���Ϳ��ڴ�С����a��ֵԽ��ԽС����֪������y��2x2�Ŀ�����С��������y����x2�Ŀ��ڵڶ�С... �Ѵ���ʽxy2��9x�ֽ���ʽ�������ȷ���ǣ� ��
A. x��y2��9�� B. x��y+3��2 C. x��y+3����y��3�� D. x��y+9����y��9��
 C
��������xy2��9x=x(y2-9)=x(y+3)(y-3),��ѡC.
C
��������xy2��9x=x(y2-9)=x(y+3)(y-3),��ѡC. ������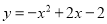 ����ƽ�Ƶõ�
����ƽ�Ƶõ�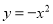 ��ƽ�Ʒ����ǣ�������
��ƽ�Ʒ����ǣ�������
A. ����ƽ��1����λ��������ƽ��1����λ
B. ����ƽ��1����λ��������ƽ��1����λ
C. ����ƽ��1����λ��������ƽ��1����λ
D. ����ƽ��1����λ��������ƽ��1����λ
 C
���������������ߵõ���������Ϊ��1��-1������ƽ�ƺ������ߵĶ�������Ϊ��0��0�������ݶ�������ı仯Ѱ��ƽ�Ʒ���Ϊ������ƽ��1����λ��������ƽ��1����λ��
��ѡ��C��
C
���������������ߵõ���������Ϊ��1��-1������ƽ�ƺ������ߵĶ�������Ϊ��0��0�������ݶ�������ı仯Ѱ��ƽ�Ʒ���Ϊ������ƽ��1����λ��������ƽ��1����λ��
��ѡ��C�� ����y=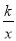 ��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A. 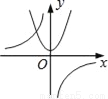 B.
B. 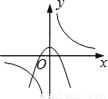 C.
C. 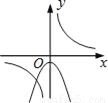 D.
D. 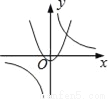
 B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
...
B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
... ���������y=x2-6x+c-2�Ķ��㵽x��ľ�����3����ôc��ֵ���ڣ�������
A. 8
B. 14
C. 8��14
D. -8��-14
 C
���������������⣬��
��
���c=8��14��
��ѡ��C��
C
���������������⣬��
��
���c=8��14��
��ѡ��C�� ��֪���κ�����ͼ���㣨0��-1������1��-3������-1��3������������κ����Ľ���ʽ��
 ������������������κ����Ľ���ʽΪ���ٰѣ�0��-1������1��-3������-1��3���ֱ����õ�����a��b��c�ķ����飬�ⷽ�������a��b��c��ֵ���Ӷ��õ����κ����Ľ���ʽ��
�������������κ����Ľ���ʽΪ��
������ã�
��ã�
�ʶ��κ����Ľ���ʽΪ��
������������������κ����Ľ���ʽΪ���ٰѣ�0��-1������1��-3������-1��3���ֱ����õ�����a��b��c�ķ����飬�ⷽ�������a��b��c��ֵ���Ӷ��õ����κ����Ľ���ʽ��
�������������κ����Ľ���ʽΪ��
������ã�
��ã�
�ʶ��κ����Ľ���ʽΪ�� �����κ���y=ax2+bx+c��x��y�IJ��ֶ�Ӧֵ���±�����x=1ʱ��y��ֵΪ��������
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
A. -27
B. -13
C. -3
D. 5
 A
������������κ����Ľ���ʽΪ��
�ߵ�x=-4��-2ʱ��y=3���������ߵĶԳ��Կ�֪h=-3��k=5��
�࣬
�ѣ�-2��3������ã�a=-2��
����κ����Ľ���ʽΪ��
��x=1ʱ��y=-27��
��ѡ��A��
A
������������κ����Ľ���ʽΪ��
�ߵ�x=-4��-2ʱ��y=3���������ߵĶԳ��Կ�֪h=-3��k=5��
�࣬
�ѣ�-2��3������ã�a=-2��
����κ����Ľ���ʽΪ��
��x=1ʱ��y=-27��
��ѡ��A�� �����(��2����3)��(5����3)����������y=ax2+bx+c�ϵĵ㣬��ô�����ߵĶԳ����� ( )
A. x=3 B. x=��3 C. x=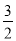 D. x=��
D. x=��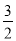
 C
����������(?2,?3)��(5,?3)����������y=ax²+bx+c�ϵĵ㣬��
(?2,?3)��(5,?3)���ڶԳ���Գƣ�
���Գ����(?2,?3)��(5,?3)���е㣬
x=��
��ѡC.
C
����������(?2,?3)��(5,?3)����������y=ax²+bx+c�ϵĵ㣬��
(?2,?3)��(5,?3)���ڶԳ���Գƣ�
���Գ����(?2,?3)��(5,?3)���е㣬
x=��
��ѡC. 
