题目内容
已知关于x的方程mx+2=x①的根是负实数,(m-2)x2+(2m-3)x-1+m=0②有实根,则m的取值是 .
考点:根的判别式,一元一次方程的解,解一元一次不等式
专题:分类讨论
分析:先根据关于x的方程mx+2=x的根是负实数得出关于m的不等式,再根据m-2)x2+(2m-3)x-1+m=0有实根可知△≥0,求出m的取值范围即可.
解答:解:∵mx+2=x,
∴x=-
,
∵方程的根是负数,
∴-
<0,解得m>1;
∵(m-2)x2+(2m-3)x-1+m=0有实根,
∴△=(2m-3)2-4(m-2)(m-1)≥0,解得m为任意实数,
∴m>1.
故答案为:m>1.
∴x=-
| 2 |
| m-1 |
∵方程的根是负数,
∴-
| 2 |
| m-1 |
∵(m-2)x2+(2m-3)x-1+m=0有实根,
∴△=(2m-3)2-4(m-2)(m-1)≥0,解得m为任意实数,
∴m>1.
故答案为:m>1.
点评:本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)中当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根是解答此题的关键.

练习册系列答案
相关题目
已知反比例函数y=
的图象经过点P(1,2),则这个函数的图象位于( )
| k |
| x |
| A、第二、三象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |

 如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.
如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.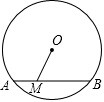 如图,⊙O的半径为5,M是
如图,⊙O的半径为5,M是
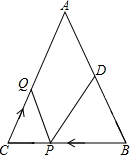 如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).
如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).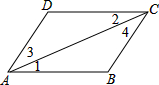 请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么?
请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么? 在直径为390mm的圆柱形油罐内装进一些油后,其横截面如图.若油的最大深度为120mm,求油面宽AB.
在直径为390mm的圆柱形油罐内装进一些油后,其横截面如图.若油的最大深度为120mm,求油面宽AB.