题目内容
20. 如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
分析 作PE⊥AB于E,求出线段AB的长,求出这辆车的速度即可判断.
解答 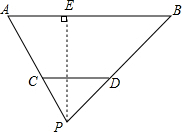 解:作PE⊥AB于E,在Rt△ABE中,∵∠A=60°,AB=60米,∠AEP=90°,
解:作PE⊥AB于E,在Rt△ABE中,∵∠A=60°,AB=60米,∠AEP=90°,
∴AE=PE÷tan30°=20$\sqrt{3}$米,
在Rt△PEB中,∵∠PEB=90°,∠B=45°,
∴BE=PE=60米,
∴AB=AE+EB=20$\sqrt{3}$+60≈94米,
∴这辆车的速度为$\frac{94}{9}$米/秒=$\frac{0.094}{9}$×3600千米/小时=37.6千米/小时,
∵37.6<60,
∴这辆车经过AB段没有超速.
点评 本题考查解直角三角形的应用、路程、速度时间之间的关系等知识,解题的关键是理解题意,学会单位换算,属于中考常考题型.

练习册系列答案
相关题目
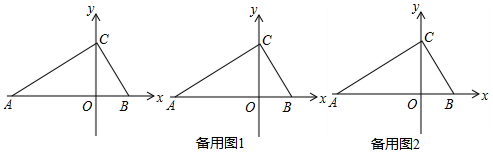
9. 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )
 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
10.红光机械厂九月份生产零件50万个,十一月份生产零件72万个,设该机械厂九、十月份生产零件数量的月平均增长率为x,则可列方程为( )
| A. | 50(1+x)2=72 | B. | 50(1-x)2=72 | C. | 72(1-x)2=50 | D. | 50×2(1+x)=72 |
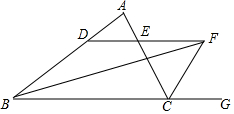 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.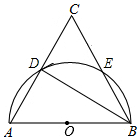 如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,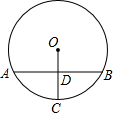 如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.
如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.