题目内容
5.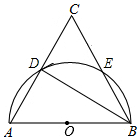 如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,(1)求证:点E是$\widehat{BD}$的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.
分析 (1)要证明点E是$\widehat{BD}$的中点只要证明BE=DE即可,根据题意可以求得BE=DE;
(2)根据题意可以求得AC和AB的长,从而可以求得⊙O的半径.
解答  (1)证明:连接AE,DE
(1)证明:连接AE,DE
∵AB是直径,
∴AE⊥BC,
∵AB=AC,
∴BE=EC,
∵∠CDB=90°,DE是斜边BC的中线,
∴DE=EB,
∴$\widehat{ED}=\widehat{EB}$,
即点E是$\widehat{BD}$的中点;
(2)设AD=x,则CD=2x,
∴AB=AC=3x,
∵AB为直径,
∴∠ADB=90°,
∴BD2=(3x)2-x2=8x2,
在Rt△CDB中,
(2x)2+8x2=122,
∴$x=2\sqrt{3}$,
∴$OA=\frac{3}{2}x=3\sqrt{3}$,
即⊙O的半径是3$\sqrt{3}$.
点评 本题考查圆心角、弦、弧的关系、等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 有理数包括正数、零和负数 | |
| B. | -a2一定是负数 | |
| C. | 34.37°=34°22′12″ | |
| D. | 两个有理数的和一定大于每一个加数 |
13.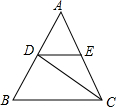 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
10.己知实数m,n满足3m2+6m-7=0,3n2+6n-7=0,且m≠n,则$\frac{1}{m}$$+\frac{1}{n}$=( )
| A. | $\frac{6}{7}$ | B. | -3 | C. | 3 | D. | 7 |
14.下列命题中,属于真命题的是( )
| A. | 圆周角等于圆心角的一半 | |
| B. | 在同一圆中,等弧所对的圆周角相等 | |
| C. | 平分弦的直线垂直于弦 | |
| D. | 过弦的中点的直线必经过圆心 |
15.25的平方根是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | ±$\sqrt{5}$ |
 如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.
如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$. 如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)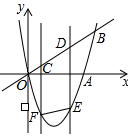 如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.
如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.