题目内容
8.某超市销售一种商品,每件商品的成本是20元.经统计销售情况发现,当这种商品的单价定为40元时,每天售出200件.在此基础上,这种商品的单价每降低1元,每天就会多售出20件.设这种商品的单价定为x元时,超市每天销售这种商品所获得的利润为y元.(1)用代数式表示,单价为x元时销售1件该商品的利润和每天销售该商品的数量;
(2)求y与x之间的函数关系式;
(3)当商品单价定为多少时,该超市每天销售这种商品获得的利润最大?最大利润为多少?
分析 (1)销售1件该商品的利润=售价-成本;每天销售该商品的数量=200+(40-x)×20;
(2)总利润y=每个面包的利润×卖出面包的个数;
(3)展开(2)中的关系式可得二次函数,利用公式法可得相应的最值问题.
解答 解:(1)这种商品的单价为x元时销售1件该商品的利润为:(x-20)元,
每天销售该商品的数量;200+20(40-x)=1000-20x(件);
(2)y=(x-20)(1000-20x)其中20≤x≤50,
(3)y=-20x2+1400x-20000,
当x=-$\frac{1400}{2×(-20)}$=35时,y最大,此时最大利润y=4500(元)..
点评 此题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件表示出:1件该商品的利润与每天的销售量.

练习册系列答案
相关题目
18.下列说法中,正确的是( )
| A. | 和等于180°的两个角叫做互为余角 | |
| B. | 一个角的补角只有一个 | |
| C. | 互补的两个角一定是一个钝角和一个锐角 | |
| D. | 同角的补角相等,等角的补角也相等 |
16.已知某圆锥的底面半径为5,母线长为8,则该圆锥的表面积为( )
| A. | 40π | B. | 50π | C. | 65π | D. | 75π |
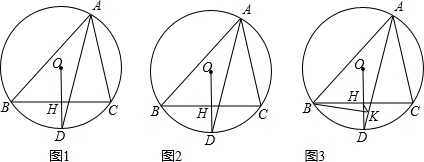
 王师傅买来九块木板,向自己做一个书架.现在有两个书架的样子,请你观察一下,再猜一猜,王师傅做的是哪个样子的书架,并说明理由.
王师傅买来九块木板,向自己做一个书架.现在有两个书架的样子,请你观察一下,再猜一猜,王师傅做的是哪个样子的书架,并说明理由. 如图,AB是⊙O的弦,直线AT经过点A,且∠CAT=∠B,AT是⊙O的切线吗?为什么?
如图,AB是⊙O的弦,直线AT经过点A,且∠CAT=∠B,AT是⊙O的切线吗?为什么?