题目内容
6.(1)已知x=$\frac{1}{2}$($\sqrt{5}+\sqrt{3}$),y=$\frac{1}{2}$($\sqrt{5}-\sqrt{3}$),求$\frac{x}{y}+\frac{y}{x}$的值(2)y=$\sqrt{1-8x}$+$\sqrt{8x-1}$$+\frac{1}{2}$,求代数式$\sqrt{\frac{x}{y}+\frac{y}{x}+2}$-$\sqrt{\frac{x}{y}+\frac{y}{x}-2}$.
分析 (1)根据x、y计算出x+y、xy的值,再将其代入到原式变形后的式子$\frac{(x+y)^{2}-2xy}{xy}$即可;
(2)二次根式的意义得出x的值,继而可得y的值,代入到原式变形后的式子$\frac{2x}{\sqrt{xy}}$即可得.
解答 解:(1)∵x=$\frac{1}{2}$($\sqrt{5}+\sqrt{3}$),y=$\frac{1}{2}$($\sqrt{5}-\sqrt{3}$),
∴x+y=$\sqrt{5}$,xy=$\frac{1}{2}$,
∴$\frac{x}{y}+\frac{y}{x}$=$\frac{{x}^{2}+{y}^{2}}{xy}$
=$\frac{(x+y)^{2}-2xy}{xy}$
=$\frac{(\sqrt{5})^{2}-2×\frac{1}{2}}{\frac{1}{2}}$
=$\frac{5-1}{\frac{1}{2}}$
=8;
(2)∵1-8x≥0且8x-1≥0,
∴x=$\frac{1}{8}$,
当x=$\frac{1}{8}$时,y=$\frac{1}{2}$,
则原式=$\sqrt{\frac{{x}^{2}+{y}^{2}+2xy}{xy}}$-$\sqrt{\frac{{x}^{2}+{y}^{2}-2xy}{xy}}$
=$\sqrt{\frac{(x+y)^{2}}{xy}}$-$\sqrt{\frac{(x-y)^{2}}{xy}}$
=$\frac{x+y}{\sqrt{xy}}$-$\frac{y-x}{\sqrt{xy}}$
=$\frac{2x}{\sqrt{xy}}$
=$\frac{2×\frac{1}{8}}{\sqrt{\frac{1}{8}×\frac{1}{2}}}$
=$\frac{\frac{1}{4}}{\frac{1}{4}}$
=1.
点评 本题主要考查二次根式的化简求值及二次根式有意义的条件,熟练根据二次根式的性质及运算法则化简各式是关键.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案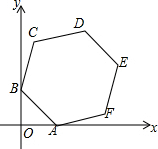 如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为2+2$\sqrt{13}$;最小值为2$\sqrt{13}$-2.
如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为2+2$\sqrt{13}$;最小值为2$\sqrt{13}$-2. 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.若OA=CD=2$\sqrt{2}$,阴影部分的面积=4-π.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.若OA=CD=2$\sqrt{2}$,阴影部分的面积=4-π.