Question

11．如图，AB是⊙O的直径，$\widehat{ED}$=$\widehat{BD}$，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．若OA=CD=2$\sqrt{2}$，阴影部分的面积=4-π．

Answer 1

分析 连接OD，得等腰直角三角形ODC，可知扇形ODB的圆心角为45°，所以利用面积差可求得阴影部分的面积．

解答 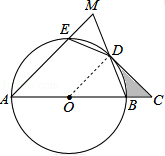解：连接OD，
∵CD是⊙O的切线，
∴OD⊥CD，
∵OA=OD，OA=CD=2$\sqrt{2}$，
∴△ODC是等腰直角三角形，
∴∠DOC=45°，
∴S_阴影=S_△ODC-S_扇形ODB，
=$\frac{1}{2}$OD•DC-$\frac{45πO{D}^{2}}{360}$，
=$\frac{1}{2}$×2$\sqrt{2}$×$2\sqrt{2}$-$\frac{45π×（2\sqrt{2}）^{2}}{360}$，
=4-π，
故答案为：4-π．

点评 本题考查了切线的性质和扇形的面积，由切线的性质可知，若出现圆的切线，必连过切点的半径，构造直角三角形；同时要熟练掌握扇形的面积公式：设圆心角是n°，圆的半径为R的扇形面积为S，则S_扇形=$\frac{nπ{R}^{2}}{360}$πR²或S_扇形=$\frac{1}{2}$lR（其中l为扇形的弧长）；对于求阴影部分的面积常用的方法有：①直接用公式法； ②和差法； ③割补法；本题就是利用和差法求阴影部分的面积．