Question

如图，两条宽度都是1cm的纸条交错地叠在一起，相交成∠α．
（1）试判断重叠部分的四边形的形状；
（2）求重叠部分的面积．

Answer 1

考点：菱形的判定与性质

专题：

分析：（1）先根据平行四边形的定义可得四边形ABCD是平行四边形，根据平行四边形的对角相等可得∠B=∠D，过点A作AE⊥BC于E，作AF⊥CD于F，然后利用“角角边”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AB=AD，再根据邻边相等的平行四边形是菱形解答；
（2）利用锐角三角函数表示出AD，再根据菱形的面积等于底乘以高列式计算即可得解．

解答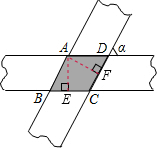：（1）解：重叠部分的四边形是菱形．
理由如下：∵两纸条对边平行，
∴AB∥CD，BC∥AD，
∴四边形ABCD是平行四边形，
∴∠B=∠D，
过点A作AE⊥BC于E，作AF⊥CD于F，
则AE=AF=1，
在△ABE和△ADF中，

∠B=∠D ∠AEB=∠AFD=90° AE=AF

，
∴△ABE≌△ADF（AAS），
∴AB=AD，
∴?ABCD是菱形，
即：重叠部分的四边形是菱形；

（2）解：如图，∠ADF=α，
AD=AF÷sinα=

1

sinα

，
∵重叠部分的四边形是菱形，
∴重叠部分的面积=

1

sinα

×1=

1

sinα

．

点评：本题考查了菱形的判定与性质，平行四边形的判定与性质，熟练掌握菱形是特殊的平行四边形是解题的关键．