题目内容
16．若$\sqrt{{{（2006-m）}^2}}+\sqrt{m-2007}=m$，则代数式m-20062的值是2007．分析 根据二次根式有意义的条件，可得出m的范围，再去掉根号，从而得出代数式m-20062的值．
解答 解：∵m-2007≥0，
∴m≥2007，
∴$\sqrt{（2006-m）^{2}}$=m-2006，
∴m-2006+$\sqrt{m-2007}$=m，
∴$\sqrt{m-2007}$=2006，
∴m-2007=20062，
∴m-20062=2007，
故答案为2007．
点评 本题考查了二次根式有意义的条件，得出m的取值范围去掉根号是解题的关键．
练习册系列答案
相关题目
11．若一个三角形的两边长分别是3和4，则第三边的长可能是（ ）
| A． | 1 | B． | 2 | C． | 7 | D． | 8 |
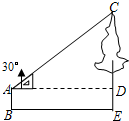如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE为5m，AB为1.5m（即小颖的眼睛距地面的距离），那么这棵树高是$\frac{10\sqrt{3}+9}{6}$m．