��Ŀ����
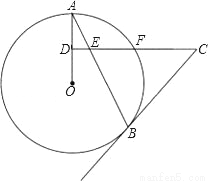
��ͼ��AB�ǡ�O���ң�DΪOA�뾶���е㣬��D��CD��OA����AB�ڵ�E������O�ڵ�F����CE=CB��
��1����֤��BC�ǡ�O�����ߣ�
��2������AF��BF�����ABF�Ķ�����
��3�����BE=10��sinA=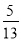 �����O�İ뾶��
�����O�İ뾶��
��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��AB�ǡ�O���ң�DΪOA�뾶���е㣬��D��CD��OA����AB�ڵ�E������O�ڵ�F����CE=CB��
��1����֤��BC�ǡ�O�����ߣ�
��2������AF��BF�����ABF�Ķ�����
��3�����BE=10��sinA=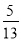 �����O�İ뾶��
�����O�İ뾶��

 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�