题目内容
 如图,学校要利用围墙建一长方形的自行车存车场,其它三面用护栏围起.其中与围墙平行的一边长(虚线部分为车场门)为(2m+3n)米(含门,门与其它护栏统一),与围墙垂直的边长比它少(m-n)米.
如图,学校要利用围墙建一长方形的自行车存车场,其它三面用护栏围起.其中与围墙平行的一边长(虚线部分为车场门)为(2m+3n)米(含门,门与其它护栏统一),与围墙垂直的边长比它少(m-n)米.(1)用m、n表示与围墙垂直的边长;
(2)求护栏的长度;
(3)若m=30,n=10,每米护栏造价80元,求建此车场所需的费用.
考点:列代数式,代数式求值
专题:
分析:(1)与围墙垂直的边长=与围墙平行的一边长-(m-n);
(2)护栏的长度=2×与围墙垂直的边长+与围墙平行的一边长;
(3)把m、n的值代入(2)中的代数式进行求值即可.
(2)护栏的长度=2×与围墙垂直的边长+与围墙平行的一边长;
(3)把m、n的值代入(2)中的代数式进行求值即可.
解答:解:(1)依题意得 (2m+3n)-(m-n)=m+4n;
(2)护栏的长度=2(m+4n)+(2m+3n)=4m+11n;
答:护栏的长度是:4m+11n.
(3)由(2)知,护栏的长度是4m+11n.则依题意得
(4×30+11×10)×80=18 400(元).
答:若m=30,n=10,每米护栏造价80元,建此车场所需的费用是18 400元.
(2)护栏的长度=2(m+4n)+(2m+3n)=4m+11n;
答:护栏的长度是:4m+11n.
(3)由(2)知,护栏的长度是4m+11n.则依题意得
(4×30+11×10)×80=18 400(元).
答:若m=30,n=10,每米护栏造价80元,建此车场所需的费用是18 400元.
点评:本题考查了列代数式和代数式求值.解题时要数形结合,该护栏的长度是由三条边组成的.

练习册系列答案
相关题目
 坡坪政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等.
坡坪政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等.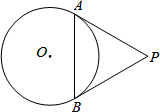 如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是
如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是 如图,已知AB⊥BD,CD⊥BD,点E、F在BC上,AF,CE相交于点O,AF=CE,BE=DF,求证:
如图,已知AB⊥BD,CD⊥BD,点E、F在BC上,AF,CE相交于点O,AF=CE,BE=DF,求证: