题目内容
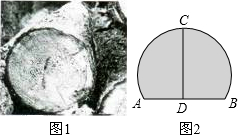某木材加工厂，把一横截面半径为12cm的圆柱形木头（如图1），据掉一部分后，放置在水平地面上，其横截面（如图2）所示，木头最高点离地面的高度CD=18cm，则木头与地面接触面的宽度AB为（ ）| A、6cm | ||
B、6
| ||
| C、12cm | ||
D、12
|
考点：垂径定理的应用,勾股定理
专题：
分析：先根据垂径定理得出AB=2AD，连接OA，根据OC=12cm求出OD的长，再根据勾股定理得出AD的长，进而可得出结论．
解答：
解：∵CD⊥AB，
∴AB=2AD，
连接OA，
∵OC=12cm，
∴OD=18-12=6cm，
在Rt△AOD中，
OA2=OD2+AD2，即122=62+AD2，解得AD=6
cm，
∴AB=2AD=12
cm．
故选D．
解：∵CD⊥AB，∴AB=2AD，
连接OA，
∵OC=12cm，
∴OD=18-12=6cm，
在Rt△AOD中，
OA2=OD2+AD2，即122=62+AD2，解得AD=6
| 3 |
∴AB=2AD=12
| 3 |
故选D．
点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图，BC是半圆O的直径，∠B=40°，则∠C=
如图所示，△ABC的面积为1，取BC边中点E作DE∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1，再取BE中点E1，作E1D1∥BF，E1F1∥EF得到四边形E1D1FF1，它的面积记作S2，照此规律作下去，S2013=
如图，阴影部分是一个正方形，该正方形的面积为（ ）cm2．| A、25 | B、5 | C、313 | D、20 |
图中直线PQ、射线AB或线段MN能相交的是（ ）
A、 |
B、 |
C、 |
D、 |
使等式
=
成立的实数m的取值范围是（ ）
|
| ||
|
A、m＞3或m＜
| ||
| B、0＜m＜3 | ||
C、m≥
| ||
| D、m＞3 |
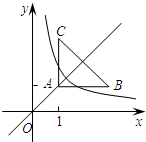如图，直角三角形ABC位于第一象限，AB=3，AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线y=| k |
| x |
| A、1≤k≤5 | ||
B、1≤k≤
| ||
C、1≤k≤
| ||
D、1≤k≤
|