题目内容
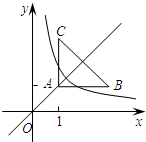 如图,直角三角形ABC位于第一象限,AB=3,AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=
如图,直角三角形ABC位于第一象限,AB=3,AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=| k |
| x |
| A、1≤k≤5 | ||
B、1≤k≤
| ||
C、1≤k≤
| ||
D、1≤k≤
|
考点:反比例函数综合题
专题:
分析:把A点的坐标代入即可求出k的最小值;当反比例函数和直线BC相交时,求出b2-4ac的值,得出k的最大值.
解答:解:在y=x中,令x=1,则y=1,则A的坐标是(1,1),
把(1,1)代入y=
得:k=1;
C的坐标是(1,3),B的坐标是(4,1),
设直线BC的解析式是y=kx+b,
则
,
解得:
,
则函数的解析式是:y=-
x+
,
根据题意,得:
=-
x+
,即2x2-11x+3k=0,
△=121-24k≥0,
解得:k≤
.
则k的范围是:1≤k≤
.
故选B.
把(1,1)代入y=
| k |
| x |
C的坐标是(1,3),B的坐标是(4,1),
设直线BC的解析式是y=kx+b,
则
|
解得:
|
则函数的解析式是:y=-
| 2 |
| 3 |
| 11 |
| 3 |
根据题意,得:
| k |
| x |
| 2 |
| 3 |
| 11 |
| 3 |
△=121-24k≥0,
解得:k≤
| 121 |
| 24 |
则k的范围是:1≤k≤
| 121 |
| 24 |
故选B.
点评:本题主要考查了反比例函数,用待定系数法求一次函数的解析式,根的判别式等知识点,解此题的关键是理解题意进而求出k的值.题目较好,难度适当.

练习册系列答案
相关题目
下列各组式子中,两个单项式是同类项的是( )
| A、2a与a2 |
| B、5a2b与a2b |
| C、xy与x2y |
| D、0.3mn2与0.3xy2 |
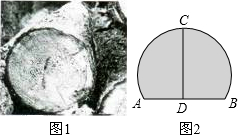 某木材加工厂,把一横截面半径为12cm的圆柱形木头(如图1),据掉一部分后,放置在水平地面上,其横截面(如图2)所示,木头最高点离地面的高度CD=18cm,则木头与地面接触面的宽度AB为( )
某木材加工厂,把一横截面半径为12cm的圆柱形木头(如图1),据掉一部分后,放置在水平地面上,其横截面(如图2)所示,木头最高点离地面的高度CD=18cm,则木头与地面接触面的宽度AB为( )| A、6cm | ||
B、6
| ||
| C、12cm | ||
D、12
|
 下列图形中,是通过(如图)平移得到的是( )
下列图形中,是通过(如图)平移得到的是( )A、 |
B、 |
C、 |
D、 |
