题目内容
 如图所示,△ABC的面积为1,取BC边中点E作DE∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1,再取BE中点E1,作E1D1∥BF,E1F1∥EF得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,S2013=
如图所示,△ABC的面积为1,取BC边中点E作DE∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1,再取BE中点E1,作E1D1∥BF,E1F1∥EF得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,S2013=考点:相似三角形的判定与性质
专题:规律型
分析:根据三角形中位线定理可求出S1的值,进而可得出S2的值,找出规律即可得出S2013的值.
解答:解:∵E是BC的中点,ED∥AB,
∴DE是△ABC的中位线,
∴DE=
AB,
∴S△DCE=
S△ABC.
同理,S△BEF=
S△ABC.
∴S1=S△ABC-S△DCE-S△BEF=
×S△ABC,
同理求得S2=
×S△ABC,
…
Sn=
×
,
S2013×S△ABC=
,
故答案为:
.
∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
∴S△DCE=
| 1 |
| 4 |
同理,S△BEF=
| 1 |
| 4 |
∴S1=S△ABC-S△DCE-S△BEF=
| 1 |
| 2 |
同理求得S2=
| 1 |
| 23 |
…
Sn=
| 1 |
| 2 |
| 1 |
| 22n-1 |
S2013×S△ABC=
| 1 |
| 24025 |
故答案为:
| 1 |
| 24025 |
点评:本题考查了三角形中位线定理、等边三角形的性质.三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
下列各组式子中,两个单项式是同类项的是( )
| A、2a与a2 |
| B、5a2b与a2b |
| C、xy与x2y |
| D、0.3mn2与0.3xy2 |
 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=
如图,△ABC中,∠C=90°,AM平分∠CAB,CM= 如图,点C,D在线段AB上,且AC=CD=DB,点E是线段DB的中点.若CE=9,则AB的长为
如图,点C,D在线段AB上,且AC=CD=DB,点E是线段DB的中点.若CE=9,则AB的长为 如图,MN为⊙O的直径,⊙O的半径为2,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为
如图,MN为⊙O的直径,⊙O的半径为2,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为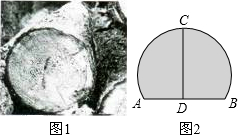 某木材加工厂,把一横截面半径为12cm的圆柱形木头(如图1),据掉一部分后,放置在水平地面上,其横截面(如图2)所示,木头最高点离地面的高度CD=18cm,则木头与地面接触面的宽度AB为( )
某木材加工厂,把一横截面半径为12cm的圆柱形木头(如图1),据掉一部分后,放置在水平地面上,其横截面(如图2)所示,木头最高点离地面的高度CD=18cm,则木头与地面接触面的宽度AB为( )